Site http://www.epsilon-publi.net/
- espace http://www.epsilon-publi.net/b/bycart/ de B. Ycart, professeur de mathématique, Université Joseph-Fourier
|
Pour visualiser le document avec epsilonwriter, cliquer ici |
Structures algébriques
Didier Piau et Bernard Ycart
Licence CC-BY
Origine : M@ths en ligne - Université Joseph Fourier
Document produit en ouvrant un fichier Tex et en copiant les images
Mots-clés: Mots-clés : relation, loi de composition, groupe, sous-groupe, noyau, puissance, ordre, anneau, corps
Sommaire
1. Introduction
L'expérience indique que l'étude abstraite des structures algébriques peut se révéler fascinante ou épuisante selon la personnalité de chacun. Un inconvénient, peut-être inévitable, de cette étude est qu'il est difficile de mettre immédiatement en relief l'utilité des résultats démontrés ; il faut passer un certain temps dans la théorie, puis de nouveau un certain temps dans des chapitres plus concrets où les résultats accumulés seront recyclés.
Tentons cependant de rassurer le lecteur grâce à la constatation suivante (à moins que cette constatation ne l'effraie encore plus) : une bonne part des résultats énoncés sur les groupes finis (concept d'ordre, théorème de Lagrange, etc.) aura l'occasion d'être mise en application dès le chapitre d'arithmétique. En effet, une première utilité de la théorie des groupes est de formaliser et systématiser les calculs usuels qu'on sait pratiquer sur les ensembles de nombres.
L'autre point de vue sur lequel on peut insister est celui des groupes formés de bijections, mais malheureusement on aura peu l'occasion de les voir vraiment appliqués dans la suite de ce cours de première année. En revanche, on peut affirmer que des connaissances sur les groupes de permutations (groupes de bijections des ensembles finis) sont bien utiles de ci de là, en informatique par exemple. Et de toutes façons l'investissement sera rentabilisé dès que le lecteur apprendra plus de géométrie, ce qui reste un cadre idéal d'usage des groupes de transformations.
2. Relations
Vous avez déjà rencontré cette notion dans votre cursus ; rappelons qu'intuitivement, une relation sur un ensemble  est la description de liens entre certains éléments de
est la description de liens entre certains éléments de  . Donnons des exemples avant même la définition.
. Donnons des exemples avant même la définition.
Exemple 1 1) La relation «est inférieur ou égal à» sur l'ensemble 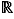 des réels : pour deux réels
des réels : pour deux réels 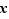 et
et 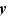 , on peut avoir
, on peut avoir 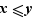 ou non.
ou non.
2) La relation «est inclus dans» sur l'ensemble des parties d'un ensemble : pour deux parties  et
et 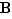 , on peut avoir
, on peut avoir 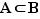 ou
ou 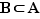 ou aucun des deux.
ou aucun des deux.
3) La relation «a le même cardinal que» sur l'ensemble des parties d'un ensemble fini.
4) Plus exotique : la relation «coïncide en au moins un point avec» pour des fonctions définies sur un même ensemble.
Définition  Le graphe d'une relation
Le graphe d'une relation 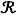 sur un ensemble
sur un ensemble  est l'ensemble des couples
est l'ensemble des couples 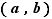 de
de 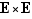 tels que
tels que 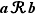 .
.
Sermon
Attention à bien lire cette définition, qui, comme toutes ses consœurs de la suite de ce cours, peut être mal retenue par de jeunes âmes peu scrupuleuses mathématiquement parlant. Il est facile de retenir que le graphe de  a un rapport avec
a un rapport avec 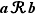 . Mais soulignons que le graphe est un ensemble.
. Mais soulignons que le graphe est un ensemble.
Profitons en pour signaler dès l'abord que les divers objets qui sont définis dans ce cours entrent dans un petit nombre de catégories : souvent des ensembles, assez souvent des applications, souvent des  -uplets (qui ne sont rien d'autres que des applications particulières, sauriez-vous préciser pourquoi ?), souvent aussi des nombres (entiers, réels ou autres), plus rarement des relations, etc. Il n'est pas difficile de savoir dans quelle catégorie ranger les graphes : ce ne sont manifestement pas des triplets, ni des nombres complexes ! Le plus important est de ne pas oublier de les ranger quelque part. Savoir à quelle catégorie appartient un objet permet d'éviter les bourdes les plus monumentales : ainsi, le symbole
-uplets (qui ne sont rien d'autres que des applications particulières, sauriez-vous préciser pourquoi ?), souvent aussi des nombres (entiers, réels ou autres), plus rarement des relations, etc. Il n'est pas difficile de savoir dans quelle catégorie ranger les graphes : ce ne sont manifestement pas des triplets, ni des nombres complexes ! Le plus important est de ne pas oublier de les ranger quelque part. Savoir à quelle catégorie appartient un objet permet d'éviter les bourdes les plus monumentales : ainsi, le symbole 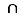 aura un sens entre deux ensembles, pas entre deux réels, et réciproquement pour le symbole
aura un sens entre deux ensembles, pas entre deux réels, et réciproquement pour le symbole 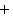 . On profitera du fait que la première phrase de cette section contient les mots «élément» et «ensemble» pour vérifier qu'on ne confond pas les deux.
. On profitera du fait que la première phrase de cette section contient les mots «élément» et «ensemble» pour vérifier qu'on ne confond pas les deux.
C'était la fin de notre sermon d'aujourd'hui.
Voici maintenant quatre définitions rébarbatives, mais incontournables.
Définition 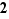 Soit
Soit  un ensemble et
un ensemble et 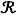 une relation sur
une relation sur  .
.
1) La relation 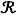 est réflexive lorsque pour tout élément
est réflexive lorsque pour tout élément  de
de  ,
, 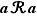 .
.
2) La relation 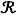 est symétrique lorsque pour tous éléments
est symétrique lorsque pour tous éléments  et
et  de
de  , si
, si 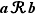 , alors
, alors 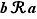 .
.
3) La relation 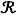 est transitive lorsque pour tous éléments
est transitive lorsque pour tous éléments  ,
,  et
et  de
de  , si
, si 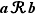 et si
et si 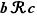 , alors
, alors 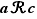 .
.
4) La relation 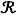 est anti-symétrique lorsque pour tous éléments
est anti-symétrique lorsque pour tous éléments  et
et  de
de  , si
, si 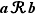 et si
et si 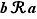 , alors
, alors 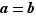 .
.
Quelques commentaires sur la dernière condition, qui est sans doute la plus difficile à bien mémoriser des quatre : c'est, comme son nom l'indique, en gros le contraire de la propriété de symétrie. La symétrie exige que quand deux éléments sont liés dans un sens, ils le sont aussi dans l'autre. L'anti-symétrie, c'est approximativement demander que si deux éléments sont liés dans un sens, ils ne le sont pas dans l'autre. Mais cette condition empêcherait un élément d'être lié à lui-même, ce qui ne serait pas désespérant en soi mais ne serait pas conforme à l'usage. De fait, l'usage s'est fait de compliquer la définition afin de garder la permission pour un élément d'être lié à lui-même.
On comprendra peut-être un peu mieux la définition en écrivant la contraposée de l'implication qu'elle contient.
Autre formulation de la définition de l'anti-symétrie Une relation 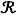 sur un ensemble
sur un ensemble  est anti-symétrique lorsque pour tous éléments
est anti-symétrique lorsque pour tous éléments  et
et  distincts de
distincts de  , on ne peut avoir simultanément
, on ne peut avoir simultanément 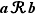 et
et 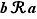 .
.
Comme nous sommes encore débutants, faisons l'effort d'expliciter une autre façon de présenter la même notion.
Autre formulation de la définition de l'anti-symétrie Une relation 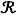 sur un ensemble
sur un ensemble  est anti-symétrique lorsque pour tous éléments
est anti-symétrique lorsque pour tous éléments  et
et  distincts de
distincts de  ,
, 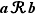 est faux ou
est faux ou 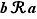 est faux.
est faux.
Bien évidemment, ce genre de liste de formulations équivalentes n'est surtout pas à «savoir par cœur». Ce qui est par contre indispensable, c'est de se familariser avec les petites manipulations qui permettent de passer de l'une à l'autre, selon les besoins.
En pratique, les relations qui pourront nous intéresser dans ce cours ne seront jamais bien compliquées ; le vocabulaire que nous avons dû ingurgiter depuis le début de ce chapitre n'a d'utilité que pour savoir reconnaître deux types très particuliers de relations : les relations d'ordre, auxquelles cette section est consacrée, puis, dans la section prochaine, les relations d'équivalence.
Définition  Une relation est une relation d'ordre lorsqu'elle est simultanément réflexive, transitive et anti-symétrique.
Une relation est une relation d'ordre lorsqu'elle est simultanément réflexive, transitive et anti-symétrique.
Considérons par exemple la relation «divise»sur l'ensemble 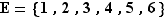 . C'est une relation d'ordre ; son graphe est visualisé par des flèches sur la figure 1.
. C'est une relation d'ordre ; son graphe est visualisé par des flèches sur la figure 1.

Intuitivement, une relation d'ordre est une relation qui peut raisonnablement être appelée «est supérieur ou égal à» ou, bien sûr, «est inférieur ou égal à».
Exemple  La relation «
La relation «  » sur
» sur 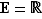 est une relation d'ordre. Pour tout ensemble
est une relation d'ordre. Pour tout ensemble  fixé, la relation «
fixé, la relation « 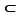 » sur
» sur 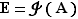 est une relation d'ordre. La seconde est sans doute plus compliquée à maîtriser que la première dans la mesure où deux parties de
est une relation d'ordre. La seconde est sans doute plus compliquée à maîtriser que la première dans la mesure où deux parties de  ne sont pas forcément comparables l'une à l'autre.
ne sont pas forcément comparables l'une à l'autre.
Le morceau est plus sérieux pour les relations d'équivalence que pour les relations d'ordre, car on ne va pas se contenter de donner une définition, mais on va aussi voir le lien avec un autre concept. Pour expliquer intuitivement ce qui va suivre, une relation d'équivalence est une relation qui peut raisonnablement s'appeler «est de la même catégorie que» et une partition est une répartition en catégories.
Définition  Une relation est une relation d'équivalence lorsqu'elle est simultanément réflexive, symétrique et transitive.
Une relation est une relation d'équivalence lorsqu'elle est simultanément réflexive, symétrique et transitive.
Exemple  L'égalité sur n'importe quel ensemble
L'égalité sur n'importe quel ensemble  fixé. La relation «a même parité que» sur l'ensemble
fixé. La relation «a même parité que» sur l'ensemble  des entiers naturels. La relation «est confondue avec ou parallèle à» sur l'ensemble des droites d'un plan affine.
des entiers naturels. La relation «est confondue avec ou parallèle à» sur l'ensemble des droites d'un plan affine.
Avalons encore trois définitions de plus en plus indigestes mais ce n'est pas gratuit, les concepts serviront plus loin, notamment en arithmétique.
Définition 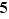 Soit
Soit 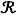 une relation d'équivalence sur un ensemble
une relation d'équivalence sur un ensemble  , et soit
, et soit  un élément de
un élément de  . On appelle classe d'équivalence de
. On appelle classe d'équivalence de  modulo
modulo 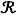 l'ensemble
l'ensemble 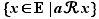
Avec des mots, la classe d'équivalence de  est l'ensemble formé des éléments de la même catégorie que
est l'ensemble formé des éléments de la même catégorie que  .
.
Notation  On note
On note 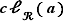 la classe d'équivalence d'un élément
la classe d'équivalence d'un élément  de
de  pour la relation d'équivalence
pour la relation d'équivalence 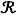 .
.
On abrège souvent 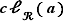 en
en 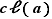 . Une autre notation pour la classe d'équivalence de
. Une autre notation pour la classe d'équivalence de  est å mais nous l'utiliserons rarement dans ce cours. Par contre, nous désignerons souvent les relations d'équivalence par le signe
est å mais nous l'utiliserons rarement dans ce cours. Par contre, nous désignerons souvent les relations d'équivalence par le signe  .
.
Sans commentaires, car il y en aura plus loin, un objet plus étrange :
Définition  Soit
Soit  une relation d'équivalence sur un ensemble
une relation d'équivalence sur un ensemble  . On appelle
. On appelle
ensemble-quotient de  par la relation
par la relation  l'ensemble :
l'ensemble : 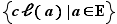
Attention tout de même ! Comme 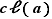 est une partie (et non un élément) de
est une partie (et non un élément) de  , l'ensemble-quotient est un ensemble de parties de
, l'ensemble-quotient est un ensemble de parties de  . Ce n'est pas une partie de
. Ce n'est pas une partie de  mais une partie de
mais une partie de 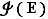 . Ce n'est pas si compliqué, mais il ne faut pas s'y perdre.
. Ce n'est pas si compliqué, mais il ne faut pas s'y perdre.
Notation  L'ensemble-quotient de
L'ensemble-quotient de  par
par  est noté
est noté 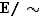 .
.
On remarquera qu'en général, chaque élément 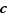 de l'ensemble quotient
de l'ensemble quotient 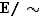 peut s'écrire comme
peut s'écrire comme 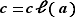 pour de nombreux éléments
pour de nombreux éléments  différents de
différents de  : très précisément,
: très précisément, 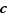 s'écrit
s'écrit 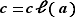 pour un élément
pour un élément  de
de  tel que
tel que 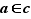 , et aussi
, et aussi 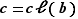 pour tous les éléments
pour tous les éléments  de
de  tels que
tels que  .
.
Définition  Une partition d'un ensemble
Une partition d'un ensemble  est un ensemble
est un ensemble  de parties de
de parties de  vérifiant les trois propriétés suivantes :
vérifiant les trois propriétés suivantes :
(i) L'ensemble vide n'est pas un élément de  .
.
(ii) Deux éléments distincts de  sont disjoints.
sont disjoints.
(iii) Tout élément de  appartient à un élément de
appartient à un élément de  .
.
C'est dur à avaler parce qu'on rentre inévitablement dans le monde des ensembles dont les éléments sont eux-mêmes des ensembles. Les éléments de  sont des parties de
sont des parties de  et doivent donc être pensés comme des groupes d'éléments de
et doivent donc être pensés comme des groupes d'éléments de  vérifiant une condition commune. Et
vérifiant une condition commune. Et  : une partition de
: une partition de  est une partie de l'ensemble des parties de
est une partie de l'ensemble des parties de  (ouf !).
(ouf !).
Exemple  En notant
En notant  l'ensemble des entiers impairs et
l'ensemble des entiers impairs et 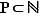 l'ensemble des entiers pairs,
l'ensemble des entiers pairs,  est une partition de
est une partition de 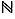 .
.
Tentons maintenant de commenter les conditions de la définition defparti. La condition (i) est sans grand intérêt et juste là pour que les énoncés marchent bien. La condition (ii) nous assure qu'on n'a inscrit aucun élément de  dans deux catégories à la fois. La condition (iii) signifie qu'on n'a oublié d'inscrire personne : tout élément de
dans deux catégories à la fois. La condition (iii) signifie qu'on n'a oublié d'inscrire personne : tout élément de  est dans un groupe.
est dans un groupe.
On remarquera qu'on peut regrouper les deux conditions significatives, ce qui donne l'énoncé suivant.
Autre formulation de la définition d'une partition Une partition d'un ensemble  est un ensemble
est un ensemble  de parties de
de parties de  vérifiant les deux propriétés (i) et (iv) ci-dessous :
vérifiant les deux propriétés (i) et (iv) ci-dessous :
(i) L'ensemble vide n'est pas un élément de  .
.
(iv) Tout élément de  appartient à un et un seul élément de
appartient à un et un seul élément de  .
.
Bien évidemment là encore il n'est pas question d'apprendre par cœur ce genre de reformulation. Il faut se convaincre, et ici ce n'est peut-être pas facile, qu'elle est bien équivalente à la précédente.
Et voici maintenant la synthèse finale, qui expliquera ce qu'est un ensemble-quotient à ceux qui ont compris ce qu'est une partition, et expliquera ce qu'est une partition à ceux qui ont compris ce qu'est un ensemble-quotient (figure 2).

Proposition  Soit
Soit 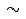 une relation d'équivalence sur un ensemble
une relation d'équivalence sur un ensemble  . L'ensemble-quotient
. L'ensemble-quotient 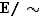 est une partition de
est une partition de  .
.
Complément Toute partition de  peut s'obtenir ainsi comme quotient par une relation d'équivalence de
peut s'obtenir ainsi comme quotient par une relation d'équivalence de  et cette relation d'équivalence est unique.
et cette relation d'équivalence est unique.
La preuve du complément est laissée au lecteur.
Démonstration : Vérifions successivement les trois propriétés définissant une partition.
Vérifions successivement les trois propriétés définissant une partition.
Vérification de (i) : Soit  un élément de
un élément de 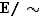 . Par définition de
. Par définition de 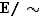 , il existe un élément
, il existe un élément  de
de  tel que
tel que  . Comme
. Comme 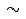 est réflexive,
est réflexive, 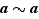 , donc
, donc  appartient à
appartient à 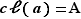 . Ainsi
. Ainsi  n'est pas réduit à l'ensemble vide.
n'est pas réduit à l'ensemble vide.
Vérification de (ii) : Soient  et
et 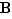 deux éléments de
deux éléments de 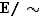 . On peut trouver des éléments
. On peut trouver des éléments  et
et  de
de  tels que
tels que  et
et 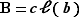 . On doit montrer que si
. On doit montrer que si  et
et 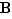 sont distincts, ils sont alors disjoints, et on va procéder par contraposition, c'est-à-dire en montrant que si
sont distincts, ils sont alors disjoints, et on va procéder par contraposition, c'est-à-dire en montrant que si  et
et 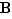 ne sont pas disjoints, ils sont égaux.
ne sont pas disjoints, ils sont égaux.
Supposons donc  et
et 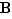 non disjoints. L'objectif est de prouver que
non disjoints. L'objectif est de prouver que  , on va montrer successivement les inclusions
, on va montrer successivement les inclusions 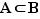 et
et 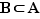 .
.
Par l'hypothèse qu'on vient de faire, on peut prendre un élément 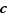 de
de  qui appartient simultanément à
qui appartient simultanément à  et à
et à 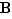 .
.
Première inclusion : Montrons tout d'abord que 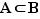 . Pour ce faire, prenons un
. Pour ce faire, prenons un 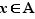 quelconque et prouvons que
quelconque et prouvons que 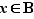 .
.
Comme 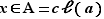 , par définition d'une classe d'équivalence, on obtient
, par définition d'une classe d'équivalence, on obtient 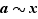 . Comme
. Comme 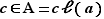 , on obtient de même
, on obtient de même 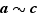 , puis, grâce à la symétrie de
, puis, grâce à la symétrie de 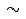 , on obtient
, on obtient 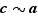 . Comme
. Comme 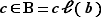 , on obtient enfin
, on obtient enfin 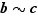 . En mettant bout à bout les trois informations ainsi obtenues (
. En mettant bout à bout les trois informations ainsi obtenues ( 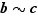 ,
, 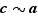 et
et 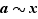 ) et en jouant deux fois sur la transitivité de
) et en jouant deux fois sur la transitivité de 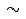 , on obtient alors que
, on obtient alors que 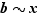 , c'est-à-dire que
, c'est-à-dire que 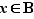 .
.
Ceci prouve bien que 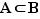 .
.
Deuxième inclusion : L'astuce est ici classique, elle consiste à remarquer que nos hypothèses (à savoir que  et
et 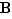 sont des classes d'équivalence, et qu'elles ne sont pas disjointes) sont symétriques en
sont des classes d'équivalence, et qu'elles ne sont pas disjointes) sont symétriques en  et
et 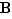 . Dès lors, en échangeant
. Dès lors, en échangeant  et
et 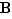 dans le morceau précédent de la preuve, on obtient bien l'inclusion
dans le morceau précédent de la preuve, on obtient bien l'inclusion 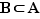 .
.
Par double inclusion, on a donc  .
.
Finalement, on a montré que si 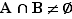 , alors
, alors  . La propriété (ii) est prouvée. Ouf, c'était le plus gros morceau !
. La propriété (ii) est prouvée. Ouf, c'était le plus gros morceau !
Vérification de (iii) : Soit  un élément de
un élément de  . Comme
. Comme 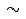 est réflexive,
est réflexive,  appartient à
appartient à 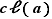 , et de ce fait on a bien trouvé un élément de
, et de ce fait on a bien trouvé un élément de 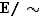 dont
dont  est lui-même élément.
est lui-même élément.
C'est fini !
3. Lois de composition et morphismes
Définition 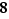 On appelle loi de composition sur un ensemble
On appelle loi de composition sur un ensemble  une application de
une application de 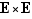 vers
vers  .
.
En fait, bien que cette définition soit générale, on n'aurait pas l'idée d'appeler «loi de composition» n'importe quelle application de 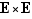 vers
vers  ; le vocable n'est utilisé que quand il est naturel de noter l'application par un symbole opératoire. Des exemples typiques de lois de composition sont l'addition
; le vocable n'est utilisé que quand il est naturel de noter l'application par un symbole opératoire. Des exemples typiques de lois de composition sont l'addition 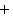 de
de  vers
vers 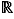 , qui associe
, qui associe 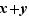 à
à 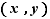 ; ou bien la loi de composition
; ou bien la loi de composition  sur l'ensemble
sur l'ensemble  des applications de
des applications de  vers
vers  , qui associe l'application
, qui associe l'application 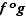 au couple d'applications
au couple d'applications 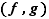 . Pour des lois de composition abstraites, le symbole opératoire
. Pour des lois de composition abstraites, le symbole opératoire  a été à la mode et nous l'utiliserons occasionnellement, surtout au début, mais nous nous contenterons rapidement de la notation multiplicative
a été à la mode et nous l'utiliserons occasionnellement, surtout au début, mais nous nous contenterons rapidement de la notation multiplicative 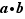 , ou même simplement
, ou même simplement 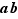 , pour l'élément obtenu en appliquant la loi de composition à
, pour l'élément obtenu en appliquant la loi de composition à 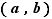 .
.
Voici un peu de vocabulaire au sujet des lois de composition.
Définition 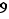 Soit
Soit  une loi de composition sur un ensemble
une loi de composition sur un ensemble  .
.
On dit que  est commutative lorsque pour tous éléments
est commutative lorsque pour tous éléments  et
et  de
de  ,
, 
On dit que  est associative lorsque pour tous éléments
est associative lorsque pour tous éléments  ,
,  et
et 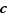 de
de  ,
, 
On dit qu'un élément  de
de  est élément neutre pour
est élément neutre pour  lorsque pour tout élément
lorsque pour tout élément  de
de  ,
, 
La cohérence de ce qui suit nécessite d'énoncer tout de suite un résultat simplissime.
Proposition 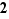 Une loi de composition possède au plus un élément neutre.
Une loi de composition possède au plus un élément neutre.
Soit 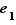 et
et 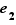 deux éléments neutres pour une loi de composition
deux éléments neutres pour une loi de composition  . Comme
. Comme 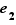 est neutre,
est neutre, 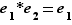 et comme
et comme 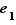 est neutre,
est neutre, 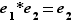 . Donc
. Donc 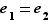 .
.
On parlera donc de l'élément neutre avec l'article défini, lorsqu'il existe un élément neutre.
Définition 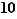 Soit
Soit  une loi de composition sur un ensemble
une loi de composition sur un ensemble  admettant un élément neutre noté
admettant un élément neutre noté  et soit
et soit  un élément de
un élément de  . On dit qu'un élément
. On dit qu'un élément  de
de  est symétrique (ou inverse) de
est symétrique (ou inverse) de  lorsque
lorsque 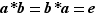
Là encore, glissons sans tarder une évidence.
Proposition  Soit
Soit  une loi de composition sur un ensemble
une loi de composition sur un ensemble  , associative et possédant un élément neutre. Chaque élément possède au plus un symétrique.
, associative et possédant un élément neutre. Chaque élément possède au plus un symétrique.
Soit  le neutre de
le neutre de  , soit
, soit  un élément de
un élément de  et soient
et soient 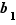 et
et 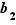 deux symétriques de
deux symétriques de  . Alors d'une part
. Alors d'une part 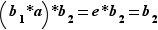 et d'autre part
et d'autre part 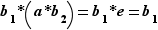 . Par associativité de la loi de composition,
. Par associativité de la loi de composition, 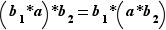 , d'où
, d'où 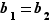 .
.
Les lois de composition intéressantes étant en pratique associatives, on pourra donc faire plein usage de la notation suivante.
Notation  Le symétrique d'un élément
Le symétrique d'un élément  est noté
est noté 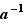 .
.
Maintenant que nous savons manipuler une loi de composition sur un seul ensemble, apprenons à évoluer d'un ensemble muni d'une loi de composition vers un autre.
Définition 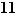 Soit
Soit  un ensemble muni d'une loi de composition
un ensemble muni d'une loi de composition  et
et 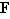 un ensemble muni d'une loi de composition
un ensemble muni d'une loi de composition  . On dit qu'une application
. On dit qu'une application 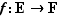 est un morphisme lorsque pour tous éléments
est un morphisme lorsque pour tous éléments  et
et  de
de  , on a l'identité :
, on a l'identité : 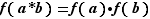
Définition 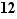 Un morphisme bijectif est appelé un isomorphisme.
Un morphisme bijectif est appelé un isomorphisme.
Il semble plus facile d'expliquer la notion d'isomorphisme que celle de morphisme en général ; deux lois de composition sur deux ensembles fourniront des structures isomorphes lorsque ces deux lois de composition agissent de la même façon, seuls les noms des éléments changeant. La phrase précédente n'étant peut-être pas si claire que cela, donnons plutôt des exemples, c'est toujours bien les exemples.
Exemple 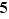 Considérons tout d'abord la bijection
Considérons tout d'abord la bijection 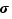 de l'ensemble
de l'ensemble  définie par
définie par 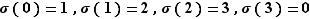 Avec à peine un peu de bon sens (tout mathématicien pense très vite à
Avec à peine un peu de bon sens (tout mathématicien pense très vite à 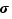 comme «faisant tourner» les quatre éléments de
comme «faisant tourner» les quatre éléments de  ), on voit sans guère de calculs que
), on voit sans guère de calculs que 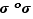 est la bijection
est la bijection 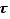 de
de  définie par
définie par 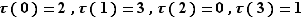 puis que
puis que  est la bijection
est la bijection 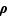 de
de  définie par
définie par 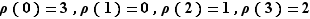 et enfin que
et enfin que 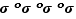 est tout simplement l'identité de
est tout simplement l'identité de  , que l'on note désormais
, que l'on note désormais  .
.
Pour abréger les calculs qui suivent, introduisons une notation.
Notation  Pour tout élément
Pour tout élément  d'un ensemble
d'un ensemble  muni d'une loi de composition
muni d'une loi de composition  et pour tout entier
et pour tout entier 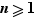 , notons
, notons  la composition de
la composition de  avec lui-même
avec lui-même  fois. Ainsi,
fois. Ainsi,  puis, pour tout
puis, pour tout 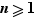 ,
, 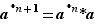 . Si la loi de composition
. Si la loi de composition  est munie d'un neutre
est munie d'un neutre  , on notera aussi
, on notera aussi  . Enfin, on abrège souvent
. Enfin, on abrège souvent  en
en 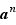 .
.
En utilisant cette notation, on peut très facilement calculer tous les produits deux à deux des bijections introduites ici ; par exemple 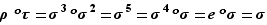 .
.
On considère alors l'ensemble 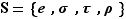 et on voit que
et on voit que  est une loi de composition sur ce sous-ensemble de
est une loi de composition sur ce sous-ensemble de  , qui sera agréablement décrite par le tableau suivant, que l'on appelle une table de composition.
, qui sera agréablement décrite par le tableau suivant, que l'on appelle une table de composition.
 |
 |
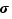 |
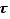 |
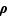 |
 |
 |
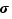 |
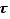 |
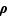 |
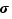 |
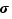 |
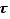 |
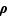 |
 |
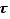 |
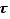 |
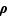 |
 |
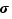 |
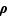 |
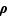 |
 |
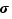 |
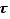 |
Considérons à présent l'ensemble des nombres complexes dont la puissance quatrième vaut  , c'est-à-dire l'ensemble
, c'est-à-dire l'ensemble 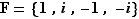 . Il est très facile de constater que la multiplication des nombres complexes définit une loi de composition sur
. Il est très facile de constater que la multiplication des nombres complexes définit une loi de composition sur 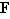 , dont la table est donnée ci-dessous.
, dont la table est donnée ci-dessous.
 |
 |
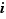 |
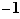 |
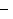 |
 |
 |
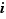 |
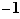 |
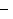 |
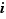 |
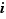 |
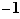 |
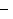 |
 |
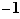 |
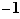 |
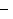 |
 |
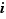 |
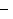 |
 |
 |
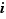 |
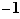 |
Visuellement, on retrouve la même table, seuls les noms des éléments ont changé. C'est signe qu'il y a un isomorphisme camouflé. On le détectera facilement ; c'est bien sûr l'application  de
de  vers
vers 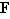 définie par :
définie par : 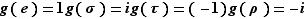
Exemple  Soit
Soit  l'ensemble des rotations de centre
l'ensemble des rotations de centre  dans le plan, et soit
dans le plan, et soit 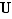 le cercle-unité de
le cercle-unité de  , c'est-à-dire l'ensemble des nombres complexes de module 1. Les lois de composition respectivement envisagées sur
, c'est-à-dire l'ensemble des nombres complexes de module 1. Les lois de composition respectivement envisagées sur 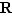 et sur
et sur 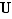 sont la composition des applications et la multiplication. On définit une application
sont la composition des applications et la multiplication. On définit une application 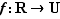 en envoyant la rotation d'angle
en envoyant la rotation d'angle 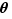 sur le nombre
sur le nombre 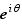 .
.
Il faut tout d'abord se soucier de vérifier que cette définition n'est pas ambiguë, car elle n'est pas loin de l'être ! Une rotation peut en effet être caractérisée par plusieurs angles (tourner d'un quart de tour dans le sens trigonométrique, c'est aussi tourner de trois quarts de tour dans le sens des aiguilles d'une montre), mais deux angles distincts 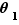 et
et 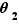 correspondant à la même bijection diffèrent d'un multiple entier de
correspondant à la même bijection diffèrent d'un multiple entier de 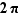 ; il existe donc un entier
; il existe donc un entier 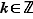 tel que
tel que  . Les valeurs
. Les valeurs  et
et  sont donc égales, et l'application
sont donc égales, et l'application  est bien définie.
est bien définie.
Une fois cette mise au point effectuée, vérifier que  est un morphisme est sans problème : si
est un morphisme est sans problème : si 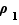 est la rotation d'angle
est la rotation d'angle 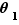 et
et 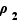 la rotation d'angle
la rotation d'angle 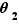 , la composée
, la composée  est la rotation
est la rotation 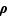 d'angle
d'angle 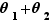 , et on a donc :
, et on a donc : 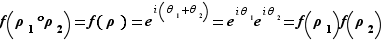 Montrer que
Montrer que  est bijective n'est pas difficile ; on en conclut que
est bijective n'est pas difficile ; on en conclut que  est un isomorphisme, en d'autres termes que l'étude des nombres complexes de module 1 nous instruira sur le fonctionnement des rotations.
est un isomorphisme, en d'autres termes que l'étude des nombres complexes de module 1 nous instruira sur le fonctionnement des rotations.
Exemple  Voici enfin un morphisme qui n'est pas un isomorphisme et qui est pourtant une simple variante du précédent. Considérons l'application
Voici enfin un morphisme qui n'est pas un isomorphisme et qui est pourtant une simple variante du précédent. Considérons l'application 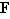 de
de 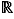 (muni de l'addition) vers
(muni de l'addition) vers 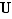 (le même qu'à l'exemple précédent, muni de la multiplication) définie par
(le même qu'à l'exemple précédent, muni de la multiplication) définie par  . On voit facilement que
. On voit facilement que 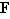 est un morphisme, mais comme, par exemple,
est un morphisme, mais comme, par exemple, 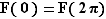 ,
, 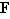 n'est pas une bijection donc pas un isomorphisme.
n'est pas une bijection donc pas un isomorphisme.
À l'évidence (et c'est sans doute ce que vous fîtes au lycée), on peut voir 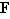 comme l'application qui «enroule» de façon régulière une corde (la droite
comme l'application qui «enroule» de façon régulière une corde (la droite  ) sur une roue (le cercle
) sur une roue (le cercle  ), encore et encore.
), encore et encore.
4. Groupes
Définition  Soit
Soit  un ensemble muni d'une loi de composition
un ensemble muni d'une loi de composition  . On dit que
. On dit que  est un groupe lorsque les trois conditions suivantes sont réalisées :
est un groupe lorsque les trois conditions suivantes sont réalisées :
(i) La loi de composition  est associative.
est associative.
(ii) La loi de composition  possède un élément neutre.
possède un élément neutre.
(iii) Tout élément de  possède un symétrique pour
possède un symétrique pour  .
.
Définition  Un groupe
Un groupe  est dit abélien (ou commutatif) lorsque sa loi de composition est commutative.
est dit abélien (ou commutatif) lorsque sa loi de composition est commutative.
Avant de donner des exemples, quelques remarques d'ordre purement calculatoire sur les groupes. Comme promis plus haut, on utilise désormais la notation multiplicative, donc 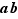 désigne le composé des éléments
désigne le composé des éléments  et
et  d'un groupe
d'un groupe  .
.
Proposition  Soit
Soit  un groupe. Alors pour tous éléments
un groupe. Alors pour tous éléments  ,
,  et
et 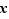 de
de  :
:
1) Si 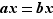 , alors
, alors 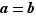 .
.
2) Si 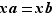 , alors
, alors 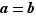 .
.
3) Le symétrique de 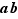 est
est 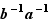 .
.
Démonstration : Il n'y a que des vérifications simples et basées sur l'associativité ; pour (1), si on suppose 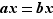 , en multipliant à droite par
, en multipliant à droite par 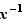 on obtient
on obtient 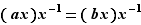 et donc
et donc 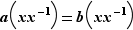 , c'est-à-dire
, c'est-à-dire 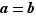 . On prouve (2) de la même façon en multipliant à gauche par
. On prouve (2) de la même façon en multipliant à gauche par 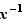 . La preuve du (3) se réduit à deux calculs élémentaires :
. La preuve du (3) se réduit à deux calculs élémentaires : 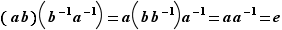 et
et  ce qui conclut la démonstration.
ce qui conclut la démonstration.
Remarque Au fait, pourquoi faut-il effectuer les deux calculs élémentaires ci-dessus ? Un seul ne suffirait-il pas ? La réponse est non ; on rappelle que 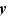 est le symétrique de
est le symétrique de 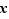 si
si 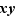 et aussi
et aussi  valent
valent  .
.
Maintenant que l'on sait calculer dans les groupes, il est temps de donner les exemples les plus élémentaires : regardons les lois de composition que nous connaissons le mieux, elles concernent les ensembles de nombres usuels.
Additions : elles sont associatives, ont un élément neutre noté 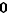 . Dans
. Dans 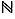 , le symétrique peut faire défaut ; ainsi
, le symétrique peut faire défaut ; ainsi 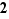 n'a pas d'opposé. Dans
n'a pas d'opposé. Dans  (puis dans les ensembles usuels bien connus), l'opposé existe. Ainsi
(puis dans les ensembles usuels bien connus), l'opposé existe. Ainsi  est un groupe pour l'addition.
est un groupe pour l'addition.
Multiplication : 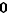 n'a jamais d'inverse, donc les ensembles de nombres bien connus ne sont jamais des groupes pour la multiplication. En revanche, si on considère le sous-ensemble formé des éléments non nuls, la multiplication y est bien définie, elle est associative et elle possède un élément neutre noté
n'a jamais d'inverse, donc les ensembles de nombres bien connus ne sont jamais des groupes pour la multiplication. En revanche, si on considère le sous-ensemble formé des éléments non nuls, la multiplication y est bien définie, elle est associative et elle possède un élément neutre noté  . Le point à problème est l'existence du symétrique (de l'inverse en notation multiplicative). Dans
. Le point à problème est l'existence du symétrique (de l'inverse en notation multiplicative). Dans 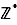 , il fait défaut à la plupart des éléments, ainsi
, il fait défaut à la plupart des éléments, ainsi 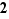 n'a pas d'inverse ;
n'a pas d'inverse ; 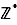 n'est donc pas un groupe. En revanche, dans
n'est donc pas un groupe. En revanche, dans 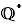 (l'ensemble des fractions non nulles) ou
(l'ensemble des fractions non nulles) ou 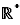 ou
ou 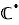 , l'existence de l'inverse ne pose pas de problème. Tous ces ensembles sont donc des groupes multiplicatifs.
, l'existence de l'inverse ne pose pas de problème. Tous ces ensembles sont donc des groupes multiplicatifs.
Encore quelques propriétés de bon sens, mais qu'il ne coûte rien d'énoncer. Elles paraissent évidentes si on comprend qu'un morphisme est moralement une application qui transporte la structure ; si elle transporte la loi de composition, elle doit aussi transporter ses caractéristiques, telles que l'élément neutre et le symétrique.
Proposition 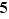 Soit
Soit  un morphisme d'un groupe
un morphisme d'un groupe  , d'élément neutre
, d'élément neutre  , vers un groupe
, vers un groupe 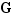 , d'élément neutre
, d'élément neutre 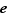 .
.
Alors 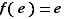 et, pour tout élément
et, pour tout élément  de
de  ,
, 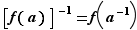 .
.
Essentiellement de la simple vérification ; pour le neutre, il s'agit d'une (petite) astuce : on calcule 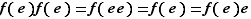 puis on simplifie par
puis on simplifie par 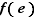 . Pour l'inverse, on fait un calcul très simple :
. Pour l'inverse, on fait un calcul très simple :  et simultanément,
et simultanément, 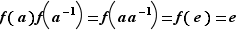 . Ceci montre bien que
. Ceci montre bien que  est l'inverse de
est l'inverse de 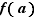 .
.
5. Exemples fondamentaux de groupes finis
Cette partie est consacrée à deux exemples fondamentaux de classes de groupes finis. La première classe est composée de groupes abéliens, la seconde de groupes non abéliens sauf dans des cas dégénérés.
Définition 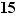 Pour tout entier
Pour tout entier 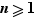 , appelons
, appelons 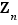 le groupe
le groupe 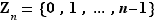 muni de la loi de composition, notée
muni de la loi de composition, notée 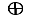 , définie comme suit. Si les éléments
, définie comme suit. Si les éléments 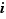 et
et 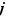 de
de 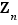 sont tels que
sont tels que 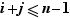 , on pose
, on pose 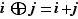 . Sinon,
. Sinon, 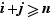 et on pose
et on pose 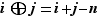 .
.
Proposition 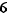 Pour tout
Pour tout 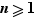 ,
, 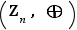 est un groupe abélien de neutre
est un groupe abélien de neutre 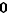 .
.
Le seul point notable est que l'inverse de 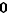 vaut
vaut 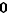 et celui d'un élément
et celui d'un élément  vaut
vaut 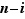 .
.
On verra plus tard une présentation plus intrinsèque des groupes 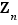 comme quotients du groupe
comme quotients du groupe  muni de l'addition. Profitons tout de même du moment pour introduire une définition.
muni de l'addition. Profitons tout de même du moment pour introduire une définition.
Définition 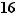 Soit
Soit  un groupe de loi de composition
un groupe de loi de composition  et de neutre
et de neutre  et soit
et soit  un élément de
un élément de  . L'ordre de
. L'ordre de  est le plus petit entier
est le plus petit entier 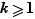 , s'il existe, tel que
, s'il existe, tel que 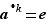 . Sinon on dit que l'ordre de
. Sinon on dit que l'ordre de  est infini.
est infini.
Bien sûr, l'ordre du neutre vaut toujours  et l'ordre de tout élément d'un groupe fini de cardinal fini
et l'ordre de tout élément d'un groupe fini de cardinal fini  est fini et inférieur ou égal à
est fini et inférieur ou égal à  . Nous verrons bientôt que c'est forcément un diviseur de
. Nous verrons bientôt que c'est forcément un diviseur de  .
.
Outre les groupes 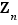 , les groupes les plus directement utilisables sont sans doute ceux qui interviennent en géométrie. Ce sont des groupes de transformations «respectant» telle ou telle propriété ; ainsi les isométries, qui conservent les distances, ou les similitudes, qui conservent les angles. Et ils constituent notre deuxième classe d'exemples.
, les groupes les plus directement utilisables sont sans doute ceux qui interviennent en géométrie. Ce sont des groupes de transformations «respectant» telle ou telle propriété ; ainsi les isométries, qui conservent les distances, ou les similitudes, qui conservent les angles. Et ils constituent notre deuxième classe d'exemples.
Tous ces groupes ont le point commun d'avoir pour loi de composition  , la composition des applications, et d'être formés de bijections.
, la composition des applications, et d'être formés de bijections.
Fondamentale (quoique très facile) sera donc l'affirmation suivante.
Proposition  Soit
Soit  un ensemble. L'ensemble des bijections de
un ensemble. L'ensemble des bijections de  dans lui-même forme un groupe pour la composition.
dans lui-même forme un groupe pour la composition.
Tout est très simple. On vérifie que, pour toute bijection  de
de  , la bijection réciproque est un symétrique de
, la bijection réciproque est un symétrique de  ; que la composée de deux bijections est une bijection, par exemple parce que
; que la composée de deux bijections est une bijection, par exemple parce que 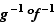 se révèle un inverse de
se révèle un inverse de 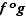 ; que la composition est associative ; et enfin que
; que la composition est associative ; et enfin que 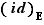 est son neutre. On a déjà fini !
est son neutre. On a déjà fini !
Notation 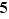 Soit
Soit  un ensemble. L'ensemble des bijections de
un ensemble. L'ensemble des bijections de  dans lui-même est noté
dans lui-même est noté 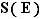 .
.
On utilise souvent (au moins en mathématiques, en informatique et en analyse du génome) le cas particulier du groupe des bijections d'un ensemble fini. L'archétype d'un tel ensemble fini étant  , cela justifie d'introduire une toute spéciale notation.
, cela justifie d'introduire une toute spéciale notation.
Notation 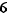 Pour tout entier
Pour tout entier 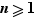 , on note
, on note 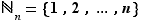 . L'ensemble des bijections de
. L'ensemble des bijections de 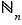 s'appelle le groupe des permutations sur
s'appelle le groupe des permutations sur  éléments. On le note
éléments. On le note 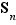 .
.
Tentons de découvrir comment fonctionne le groupe des permutations 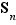 pour
pour  pas trop gros ; il vaut même mieux prendre
pas trop gros ; il vaut même mieux prendre  franchement petit, car
franchement petit, car 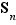 possédant
possédant 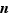 éléments, on serait vite débordé.
éléments, on serait vite débordé.
Pour  , le groupe n'a qu'un élément ; sa table est vite tracée.
, le groupe n'a qu'un élément ; sa table est vite tracée.
 |
 |
 |
 |
Pour 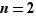 , il y a deux bijections de
, il y a deux bijections de 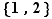 : celle qui échange les deux éléments, qu'on notera
: celle qui échange les deux éléments, qu'on notera 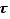 , et l'identité.
, et l'identité.
La table du groupe est donc la suivante.
 |
 |
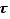 |
 |
 |
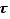 |
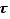 |
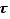 |
 |
À partir de 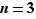 , les calculs complets seraient nettement plus fastidieux. On va en profiter pour introduire des notations et énumérer les ensembles
, les calculs complets seraient nettement plus fastidieux. On va en profiter pour introduire des notations et énumérer les ensembles 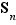 .
.
Notation  On dispose de plusieurs notations pour désigner une permutation
On dispose de plusieurs notations pour désigner une permutation 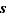 élément de
élément de 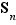 . La première est
. La première est
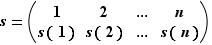
que l'on abrège parfois en 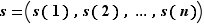
Définition  Une orbite d'une permutation
Une orbite d'une permutation 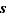 élément de
élément de 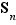 est une partie
est une partie 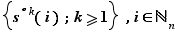
On peut expliciter la structure des orbites comme suit.
Proposition  Pour toute permutation
Pour toute permutation 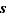 et tout élément
et tout élément 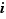 de
de 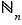 , il existe un entier
, il existe un entier 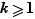 tel que
tel que 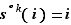 . Le plus petit entier
. Le plus petit entier 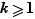 qui vérifie cette propriété est le cardinal de l'orbite de
qui vérifie cette propriété est le cardinal de l'orbite de 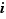 et s'appelle la taille de l'orbite de
et s'appelle la taille de l'orbite de 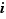 .
.
Définition 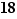 Un cycle
Un cycle 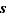 est un élément de
est un élément de 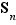 qui possède exactement une orbite de longueur différente de
qui possède exactement une orbite de longueur différente de  .
.
Pour tout cycle 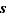 de longueur
de longueur 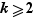 , il existe donc une partie
, il existe donc une partie 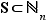 de cardinal
de cardinal  telle que
telle que  pour tout élément
pour tout élément 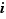 de
de 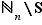 . De plus, on peut numéroter les éléments de
. De plus, on peut numéroter les éléments de 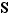 comme suit :
comme suit : 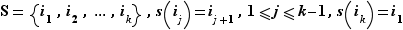
Notation 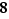 On désigne le cycle
On désigne le cycle 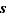 de longueur
de longueur 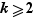 ci-dessus par l'écriture
ci-dessus par l'écriture 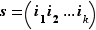
Avertissement On aura remarqué que la notation n.cyc est affreusement proche de l'écriture abrégée d'une permutation quelconque donnée dans la notation n.perm, la seule différence portant sur la présence ou l'absence de virgules.
Bien sûr, si le nombre d'entiers figurant dans l'écriture de 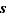 est différent de
est différent de  , on désigne forcément le cycle. Dans le cas contraire, on veillera à ne pas confondre
, on désigne forcément le cycle. Dans le cas contraire, on veillera à ne pas confondre 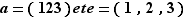 puisque
puisque  est un cycle de longueur
est un cycle de longueur  et
et  est la permutation identité.
est la permutation identité.
Enfin, remarquons qu'un cycle dispose de plusieurs écritures différentes, par exemple 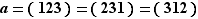 Fin de l'avertissement.
Fin de l'avertissement.
Il est à présent facile d'énumérer les éléments de 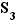 : outre l'identité, que l'on va noter
: outre l'identité, que l'on va noter  , il y en a trois d'apparence identique : l'un, que je noterai
, il y en a trois d'apparence identique : l'un, que je noterai  , échange
, échange  et
et 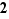 en laissant
en laissant  fixe ; un autre, que je me garderai astucieusement de noter, échange
fixe ; un autre, que je me garderai astucieusement de noter, échange 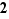 et
et  en laissant
en laissant  fixe ; le dernier échange
fixe ; le dernier échange  et
et  en laissant
en laissant 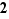 fixe. Enfin deux autres jouent aussi des rôles voisins : l'un, que je noterai
fixe. Enfin deux autres jouent aussi des rôles voisins : l'un, que je noterai  , fait «tourner» les trois éléments de
, fait «tourner» les trois éléments de 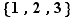 en envoyant
en envoyant  sur
sur 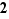 ,
, 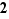 sur
sur  , et
, et  sur
sur  ; l'autre, dont je remarquerai que c'est le carré de
; l'autre, dont je remarquerai que c'est le carré de  , les fait «tourner» dans l'autre sens. Ainsi,
, les fait «tourner» dans l'autre sens. Ainsi,
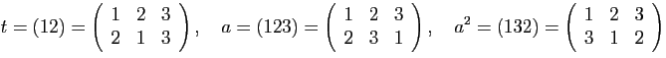
On va remplir la table du groupe par ajouts successifs d'information. L'information la plus récente sera systématiquement portée en gras.
Au point où nous en sommes, il est facile de commencer en remarquant que 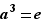 tandis que
tandis que  , comme on l'a déjà dit, est distinct de
, comme on l'a déjà dit, est distinct de  . En outre les trois autres éléments ont un carré égal à
. En outre les trois autres éléments ont un carré égal à  .
.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
C'est le bon moment pour glisser une remarque importante : dans la table de composition d'un groupe on trouve chaque élément du groupe une fois et une seule dans chaque ligne, et dans chaque colonne. Sauriez-vous le démontrer ? Sinon, cher lecteur, nous vous conseillons d'arrêter votre lecture et de chercher une démonstration.
Le produit  ne peut être présent deux fois dans la colonne
ne peut être présent deux fois dans la colonne  , ni deux fois dans la ligne
, ni deux fois dans la ligne  . Il est donc distinct des éléments qui y figurent déjà, c'est-à-dire de
. Il est donc distinct des éléments qui y figurent déjà, c'est-à-dire de  , de
, de  , de
, de  et de
et de  . C'est donc un cinquième élément, qu'on peut alors faire figurer dans la cinquième ligne et la cinquième colonne du tableau. On calcule au passage sans mal
. C'est donc un cinquième élément, qu'on peut alors faire figurer dans la cinquième ligne et la cinquième colonne du tableau. On calcule au passage sans mal  , et
, et 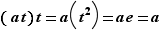 .
.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Puis à son tour,  ne peut déjà figurer dans la ligne
ne peut déjà figurer dans la ligne  ni dans la colonne
ni dans la colonne  : c'est donc le sixième élément. On peut l'ajouter au tableau en complétant par quelques calculs évidents.
: c'est donc le sixième élément. On peut l'ajouter au tableau en complétant par quelques calculs évidents.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
En utilisant toujours l'astuce selon laquelle il ne peut y avoir deux fois la même valeur dans une ligne ni dans une colonne, on arrive à calculer 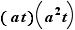 et
et 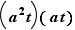 par simple élimination de cinq valeurs impossibles.
par simple élimination de cinq valeurs impossibles.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Surprise ! On vient de montrer avec une étonnante économie de calculs que le groupe n'est pas commutatif ; en effet 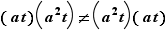 .
.
Le même truc des répétitions interdites permet de compléter le coin inférieur droit du tableau.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Dernier obstacle inattendu, alors que nous avions presque fini, avec la méthode, maintenant classique pour nous, de remplir les cases par élimination, cette méthode est insuffisante pour remplir les six misérables cases laissées blanches ! Il faut une nouvelle astuce pour passer cet obstacle. Concentrons-nous sur la case correspondant au produit 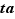 . Pour calculer ce produit, bidouillons un peu :
. Pour calculer ce produit, bidouillons un peu : 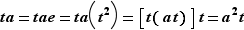 . Une nouvelle case est remplie :
. Une nouvelle case est remplie :
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Cette étape franchie, il est désormais très facile de finir de remplir la table en utilisant l'idée simple : pas plus d'une apparition par ligne ou par colonne.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
On a donc obtenu la table complète de la loi de composition  sur
sur 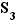 , en n'utilisant que des techniques élémentaires.
, en n'utilisant que des techniques élémentaires.
6. Sous-groupes
Maintenant que nous connaissons ce que nous avons pompeusement appelé les exemples fondamentaux, il reste à apprendre à tirer de ces exemples trop fondamentaux pour être vraiment utiles des exemples plus concrets.
Pour cela, introduisons une nouvelle notion.
Définition  Soit
Soit  un groupe. On dit qu'un sous-ensemble
un groupe. On dit qu'un sous-ensemble  de
de  est un sous-groupe de
est un sous-groupe de  lorsque les trois conditions suivantes sont vérifiées :
lorsque les trois conditions suivantes sont vérifiées :
(i) L'ensemble  n'est pas vide.
n'est pas vide.
(ii) Pour tous  et
et  de
de  , le produit
, le produit 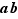 est aussi dans
est aussi dans  .
.
(iii) Pour tout  de
de  , l'inverse
, l'inverse 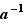 de
de  est aussi dans
est aussi dans  .
.
Avant de commenter ce que ça veut dire, donnons tout de suite une proposition très simple, et utile en pratique pour vérifier qu'un sous-ensemble d'un groupe est un sous-groupe.
Proposition 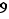 Soit
Soit  un groupe. Un sous-ensemble
un groupe. Un sous-ensemble  de
de  est un sous-groupe de
est un sous-groupe de  si et seulement si les deux conditions suivantes sont vérifiées :
si et seulement si les deux conditions suivantes sont vérifiées :
(i) L'ensemble  n'est pas vide.
n'est pas vide.
(iv) Pour tous  et
et  de
de  , le produit
, le produit 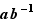 est aussi dans
est aussi dans  .
.
Supposons que  est un sous-groupe de
est un sous-groupe de  , c'est-à-dire qu'il vérifie (i), (ii) et (iii). Il est alors clair que (i) est vérifiée.
, c'est-à-dire qu'il vérifie (i), (ii) et (iii). Il est alors clair que (i) est vérifiée.
Montrons que  vérifie (iv). Soit
vérifie (iv). Soit  et
et  deux éléments de
deux éléments de  . En appliquant (iii) à
. En appliquant (iii) à  , on constate que
, on constate que  est aussi dans
est aussi dans  , puis en appliquant (ii) à
, puis en appliquant (ii) à  et
et  que le produit
que le produit 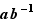 aussi. Cette partie de la preuve est déjà finie !
aussi. Cette partie de la preuve est déjà finie !
Supposons maintenant que  vérifie (i) et (iv). Vérifier (i) est bien sûr sans problème. Avant de montrer que
vérifie (i) et (iv). Vérifier (i) est bien sûr sans problème. Avant de montrer que  vérifie (ii) et (iii), montrons préalablement que
vérifie (ii) et (iii), montrons préalablement que  appartient à
appartient à  , où
, où  désigne l'élément neutre de
désigne l'élément neutre de  . En effet
. En effet  n'étant pas vide, on peut prendre un élément
n'étant pas vide, on peut prendre un élément 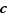 dans
dans  , puis appliquer l'hypothèse (iv) à
, puis appliquer l'hypothèse (iv) à 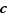 et
et 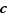 pour conclure que
pour conclure que 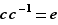 appartient à
appartient à  .
.
Montrons maintenant que  vérifie (iii). Soit
vérifie (iii). Soit  un élément de
un élément de  . Puisqu'on sait maintenant que
. Puisqu'on sait maintenant que  aussi est dans
aussi est dans  , on peut appliquer (iv) à
, on peut appliquer (iv) à  et
et  pour obtenir
pour obtenir 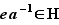 , c'est-à-dire
, c'est-à-dire  .
.
Montrons enfin que  vérifie (ii). Soit
vérifie (ii). Soit  et
et  deux éléments de
deux éléments de  . Par la propriété (iii) appliquée à
. Par la propriété (iii) appliquée à  ,
, 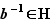 , puis par la propriété (iv) appliquée à
, puis par la propriété (iv) appliquée à  et
et  ,
, 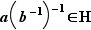 , c'est-à-dire
, c'est-à-dire 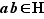 .
.
Bien que le résultat qui suive soit très simple à démontrer, son importance lui fait mériter l'appellation de :
Théorème  Soit
Soit  un groupe et
un groupe et  un sous-groupe de
un sous-groupe de  . La restriction à
. La restriction à  de la loi de composition sur
de la loi de composition sur  fait de
fait de  un groupe.
un groupe.
Il ne faut pas manquer de vérifier la possibilité de restreindre la loi de composition initiale, application de 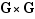 vers
vers  à une loi de composition sur
à une loi de composition sur  , c'est-à-dire une application de
, c'est-à-dire une application de 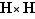 vers
vers  . Comme on veut restreindre non seulement l'ensemble de départ mais aussi l'ensemble d'arrivée, on est dans la situation où il faut spécialement prendre garde. Mais la propriété (ii) de la définition des «sous-groupes» assure précisément que la loi de composition de
. Comme on veut restreindre non seulement l'ensemble de départ mais aussi l'ensemble d'arrivée, on est dans la situation où il faut spécialement prendre garde. Mais la propriété (ii) de la définition des «sous-groupes» assure précisément que la loi de composition de  envoie l'ensemble
envoie l'ensemble  dans
dans  et que la restriction a donc bien un sens.
et que la restriction a donc bien un sens.
L'associativité de cette restriction est alors évidente. Dans la preuve de la proposition précédente, on a montré au passage que le neutre de  était élément de
était élément de  . Il est alors évidemment neutre pour la loi de composition restreinte à
. Il est alors évidemment neutre pour la loi de composition restreinte à  . Enfin la propriété (iii) garantit l'existence d'un symétrique pour chaque élément de
. Enfin la propriété (iii) garantit l'existence d'un symétrique pour chaque élément de  .
.
Voyons maintenant comment ce théorème permet de fabriquer plein de groupes nouveaux et intéressants.
Exemple 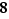 Soit
Soit  le groupe des bijections strictement croissantes de
le groupe des bijections strictement croissantes de 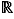 vers
vers 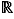 , muni de la composition. Montrer que
, muni de la composition. Montrer que  est un groupe.
est un groupe.
(On rappellera, au cas où ce serait nécessaire, qu'une application  est dite strictement croissante lorsque pour tous
est dite strictement croissante lorsque pour tous 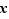 et
et 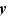 ,
, 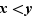 entraîne
entraîne 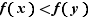 ).
).
La bonne idée est de montrer que  est un sous-groupe du groupe
est un sous-groupe du groupe 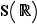 . Lançons-nous.
. Lançons-nous.
La vérification de (i) est évidente : il est clair que l'application identique est une bijection strictement croissante de 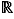 sur
sur 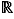 .
.
Passons à (ii). Soit  et
et  deux bijections strictement croissantes de
deux bijections strictement croissantes de 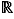 sur
sur 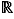 . On sait déjà que
. On sait déjà que 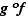 est une bijection ; montrons qu'elle est strictement croissante. Soit
est une bijection ; montrons qu'elle est strictement croissante. Soit 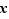 et
et 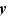 deux réels avec
deux réels avec 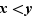 ; alors
; alors 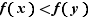 (croissance de
(croissance de  ) puis
) puis 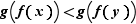 (croissance de
(croissance de  ). Ceci montre bien que
). Ceci montre bien que 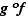 est strictement croissante.
est strictement croissante.
Vérifions enfin (iii). Soit  une bijection strictement croissante de
une bijection strictement croissante de 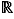 vers
vers 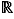 . Il est bien clair que
. Il est bien clair que 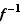 est bijective ; vérifions qu'elle est strictement croissante. Soit
est bijective ; vérifions qu'elle est strictement croissante. Soit 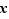 et
et 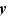 deux réels avec
deux réels avec 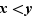 . On ne peut avoir
. On ne peut avoir 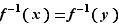 , car
, car 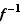 est injective ; on ne peut avoir
est injective ; on ne peut avoir  , car
, car  étant strictement croissante on en déduirait l'inégalité
étant strictement croissante on en déduirait l'inégalité 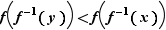 , qui est fausse. Par élimination on a donc bien
, qui est fausse. Par élimination on a donc bien 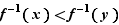 .
.
Exemple  Soit
Soit  un sous-ensemble de
un sous-ensemble de  et
et  l'ensemble des isométries
l'ensemble des isométries  de
de  sur
sur  telles que
telles que 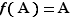 . On montrerait par le même genre de méthode que
. On montrerait par le même genre de méthode que  est un groupe parce que c'est un sous-groupe de
est un groupe parce que c'est un sous-groupe de  . Dès que
. Dès que  sera un peu trop patatoïdal,
sera un peu trop patatoïdal,  se réduira à
se réduira à 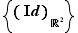 et sera donc peu intéressant, mais si
et sera donc peu intéressant, mais si  possède des symétries raisonnables, par exemple si
possède des symétries raisonnables, par exemple si  est un pentagone régulier, le groupe
est un pentagone régulier, le groupe  méritera notre attention.
méritera notre attention.
Le théorème de Lagrange est un résultat simple et élégant, proposé ici surtout pour le plaisir de faire une démonstration agréable.
Théorème 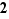 [de Lagrange] Soit
[de Lagrange] Soit  un groupe fini et
un groupe fini et  un sous-groupe de
un sous-groupe de  . Alors le nombre d'éléments de
. Alors le nombre d'éléments de  divise le nombre d'éléments de
divise le nombre d'éléments de  .
.
Elle repose sur l'introduction de la relation  définie pour tous éléments
définie pour tous éléments 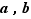 de
de  par :
par : 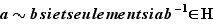 Le plan de la preuve est le suivant :
Le plan de la preuve est le suivant :
On vérifie que 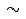 , comme son nom le laisse penser, est une relation d'équivalence.
, comme son nom le laisse penser, est une relation d'équivalence.
On vérifie que toutes les classes d'équivalence pour la relation 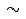 ont le même nombre d'éléments, à savoir le nombre d'éléments de
ont le même nombre d'éléments, à savoir le nombre d'éléments de  .
.
On conclut en quelques mots.
Exécution...
Étape 1. Vérifions successivement les trois propriétés requises des relations d'équivalence.
Soit  un élément de
un élément de  . Comme
. Comme 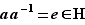 ,
, 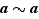 . La relation
. La relation 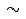 est donc réflexive.
est donc réflexive.
Soit  et
et  deux éléments de
deux éléments de  , avec
, avec  , donc
, donc 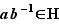 . En prenant l'inverse,
. En prenant l'inverse, 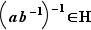 , c'est-à-dire
, c'est-à-dire 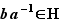 , soit
, soit 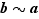 : la relation
: la relation 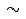 est donc symétrique.
est donc symétrique.
Soit  ,
,  et
et  trois éléments de
trois éléments de  , avec
, avec  et
et 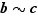 . On a donc
. On a donc 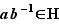 et
et 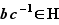 . En multipliant entre eux ces deux éléments de
. En multipliant entre eux ces deux éléments de  , on obtient que
, on obtient que 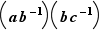 appartient à
appartient à  , c'est-à-dire
, c'est-à-dire 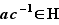 , soit
, soit 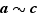 . La relation
. La relation 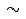 est donc transitive.
est donc transitive.
La relation 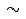 est donc une relation d'équivalence.
est donc une relation d'équivalence.
Étape 2. Soit  un élément fixé de
un élément fixé de  . L'objectif est de montrer que sa classe d'équivalence
. L'objectif est de montrer que sa classe d'équivalence 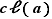 possède le même nombre d'éléments que
possède le même nombre d'éléments que  . Pour ce faire, une bonne idée serait de montrer qu'il existe une bijection entre
. Pour ce faire, une bonne idée serait de montrer qu'il existe une bijection entre 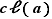 et
et  . Et pour montrer qu'une bijection existe, une bonne idée pourrait être d'en sortir une de sa manche (en mathématiques, on dit «exhiber»), et voir qu'elle convient !
. Et pour montrer qu'une bijection existe, une bonne idée pourrait être d'en sortir une de sa manche (en mathématiques, on dit «exhiber»), et voir qu'elle convient !
Introduisons donc l'application 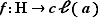 définie par : pour tout
définie par : pour tout  de
de  ,
,  Vérifions tout d'abord que
Vérifions tout d'abord que  est bien une application. La difficulté vient ici de ce que la formule
est bien une application. La difficulté vient ici de ce que la formule 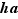 possède certes un sens, mais qu'il faudrait savoir que
possède certes un sens, mais qu'il faudrait savoir que 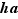 appartient bien à
appartient bien à 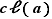 . Heureusement, la question est plus facile à résoudre qu'à poser ! C'est en effet une simple vérification :
. Heureusement, la question est plus facile à résoudre qu'à poser ! C'est en effet une simple vérification : 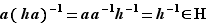 ; donc
; donc 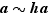 ; en d'autres termes
; en d'autres termes 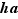 appartient à
appartient à 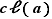 .
.
Vérifions que  est une bijection. Soit
est une bijection. Soit  un élément de
un élément de  tel que
tel que  . Cherchons les antécédents de
. Cherchons les antécédents de  . Un élément
. Un élément  de
de  est antécédent de
est antécédent de  par
par  si et seulement si
si et seulement si  , c'est-à-dire si et seulement si
, c'est-à-dire si et seulement si 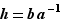 . Il y a donc au plus un antécédent, à savoir
. Il y a donc au plus un antécédent, à savoir 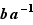 , et comme en outre
, et comme en outre 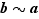 , l'élément
, l'élément 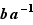 est dans
est dans  et il y a exactement un antécédent.
et il y a exactement un antécédent.
Ceci montre que  est une bijection, et
est une bijection, et 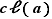 compte donc exactement autant d'éléments que
compte donc exactement autant d'éléments que  .
.
Étape 3. Il ne reste plus qu'à conclure. On dispose d'une relation d'équivalence 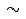 , donc d'un ensemble-quotient
, donc d'un ensemble-quotient 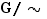 , qui constitue une partition de
, qui constitue une partition de  . Chacune des parties de
. Chacune des parties de  figurant dans cette partition possède exactement
figurant dans cette partition possède exactement 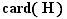 éléments ; le nombre total d'éléments de
éléments ; le nombre total d'éléments de  est donc égal au produit de
est donc égal au produit de 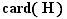 par le nombre de parties de
par le nombre de parties de  figurant dans la partition
figurant dans la partition 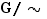 et est en particulier un multiple de
et est en particulier un multiple de 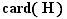 .
.
7. Noyaux
Une petite définition, à l'usage pratique pour prouver des injectivités. Pour le reste, une section courte sans guère de commentaires.
Définition 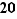 Soit
Soit  un morphisme de groupes, allant d'un groupe
un morphisme de groupes, allant d'un groupe  vers un groupe
vers un groupe 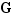 , dont l'élément neutre est noté
, dont l'élément neutre est noté 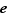 . Le noyau de
. Le noyau de  est par définition l'ensemble des éléments
est par définition l'ensemble des éléments 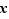 de
de  tels que
tels que 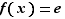 .
.
Notation  Le noyau de
Le noyau de  est noté
est noté 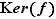 (parce que
(parce que 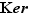 est l'abréviation de l'allemand «Kern»).
est l'abréviation de l'allemand «Kern»).
Le fait suivant est presque évident, mais on ne peut s'interdire de le souligner.
Proposition 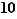 Le noyau d'un morphisme est un sous-groupe du groupe de départ.
Le noyau d'un morphisme est un sous-groupe du groupe de départ.
Soit  un morphisme d'un groupe noté
un morphisme d'un groupe noté  de neutre noté
de neutre noté  vers un groupe noté
vers un groupe noté 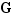 de neutre noté
de neutre noté 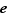 .
.
On sait que 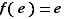 donc
donc 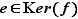 , qui n'est donc pas vide.
, qui n'est donc pas vide.
Soit  et
et  deux éléments de
deux éléments de 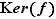 . On a alors
. On a alors 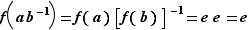 , donc
, donc 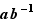 appartient à
appartient à 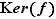 .
.
Proposition  Soit
Soit  un morphisme de groupes, le neutre du groupe de départ étant noté
un morphisme de groupes, le neutre du groupe de départ étant noté  . L'application
. L'application  est injective si et seulement si
est injective si et seulement si 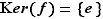 .
.
Sans surprise, vérifions successivement les deux implications. On notera 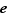 le neutre du groupe d'arrivée.
le neutre du groupe d'arrivée.
Preuve de l'implication directe.
Supposons  injective. On sait déjà que
injective. On sait déjà que 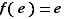 , et donc que
, et donc que 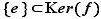 . Réciproquement, si
. Réciproquement, si 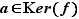 ,
, 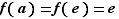 , et comme
, et comme  est injective,
est injective, 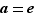 . D'où l'égalité
. D'où l'égalité 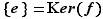 .
.
Preuve de l'implication réciproque.
Supposons que 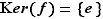 . Soit
. Soit  et
et  deux éléments du groupe de départ vérifiant
deux éléments du groupe de départ vérifiant 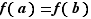 . Alors
. Alors 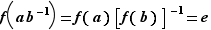 , donc
, donc  , donc
, donc 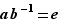 , donc
, donc 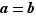 . Donc
. Donc  est injective.
est injective.
8. Puissances et ordre d'un élément d'un groupe
Rappelons une définition déjà utilisée en partie.
Définition 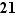 Soit
Soit  un élément d'un groupe et
un élément d'un groupe et  un entier relatif. On appelle puissance
un entier relatif. On appelle puissance  -ième de
-ième de  l'élément
l'élément 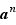 défini comme valant
défini comme valant 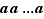 (n fois) si
(n fois) si 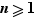 , comme valant l'inverse de
, comme valant l'inverse de 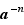 si
si 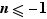 et comme valant l'élément neutre si
et comme valant l'élément neutre si 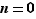 .
.
Définition équivalente (évitant l'emploi des trois petits points) On définit par récurrence 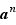 pour tout entier
pour tout entier  positif ou nul en posant
positif ou nul en posant 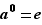 puis, pour tout
puis, pour tout  ,
, 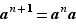 , puis on définit directement
, puis on définit directement 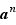 pour tout entier
pour tout entier  négatif en posant
négatif en posant 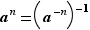 (puisque
(puisque 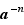 est alors déjà défini).
est alors déjà défini).
Notation  L'ensemble des puissances de
L'ensemble des puissances de  est noté
est noté 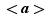
Proposition  Soit
Soit  un élément d'un groupe et
un élément d'un groupe et  et
et 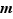 deux entiers ; alors
deux entiers ; alors 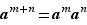 et
et 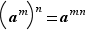 .
.
C'est très simple à voir avec des points de suspension, en n'oubliant pas de distinguer plein de cas selon les signes des divers entiers des formules, la définition dépendant de ce signe. Comme c'est à la fois très facile et très fastidieux, on va oublier discrètement de le faire.
On en déduit aussitôt la très élémentaire
Proposition  Soit
Soit  un groupe, et
un groupe, et  un élément de
un élément de  . L'ensemble
. L'ensemble 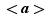 est un sous-groupe de
est un sous-groupe de  .
.
L'ensemble 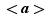 n'est pas vide, puisqu'il contient
n'est pas vide, puisqu'il contient  . Si
. Si 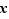 et
et 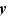 sont deux éléments de
sont deux éléments de 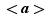 , on peut trouver deux entiers (relatifs)
, on peut trouver deux entiers (relatifs) 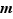 et
et  permettant d'écrire
permettant d'écrire 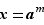 et
et 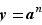 . Dès lors
. Dès lors 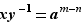 et donc
et donc  appartient à
appartient à 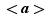 .
.
Définition 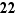 Soit
Soit  un élément d'un groupe, dont le neutre est noté
un élément d'un groupe, dont le neutre est noté  . Si pour tout
. Si pour tout 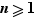 ,
, 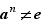 on dit que
on dit que  est d'ordre infini. Sinon on appelle ordre de
est d'ordre infini. Sinon on appelle ordre de  le plus petit entier
le plus petit entier 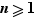 tel que
tel que 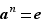 .
.
Afin de tenter de prévenir les confusions, introduisons un autre sens du mot «ordre», pas du tout synonyme du précédent et un peu superflu mais tellement passé dans les usages qu'on ne peut l'éviter.
Définition  Soit
Soit  un groupe fini. L'ordre de
un groupe fini. L'ordre de  est son cardinal.
est son cardinal.
Histoire d'appliquer rétroactivement la division euclidienne, qui sera correctement définie dans le chapitre sur l'arithmétique, démontrons le
Théorème  Soit
Soit  un élément d'un groupe. L'ordre de
un élément d'un groupe. L'ordre de  est égal au nombre d'éléments de
est égal au nombre d'éléments de 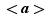 .
.
La preuve étant plus longue que la moyenne, essayons de dégager des étapes intermédiaires avec des énoncés précis, qui nous permettront de souffler quand ils seront atteints. On notera  l'élément neutre du groupe considéré.
l'élément neutre du groupe considéré.
Étape intermédiaire 1 : si l'ordre de  est fini, noté
est fini, noté  ,
, 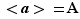 où on a posé
où on a posé 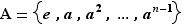
Preuve de l'étape 1. Soit  un élément de
un élément de 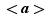 , c'est-à-dire une puissance de
, c'est-à-dire une puissance de  . On peut donc mettre
. On peut donc mettre  sous forme
sous forme 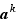 pour un entier relatif
pour un entier relatif  . Effectuons la division euclidienne de
. Effectuons la division euclidienne de  par
par  , ainsi
, ainsi 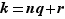 , avec
, avec 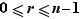 . On a alors
. On a alors 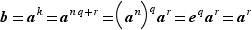 donc
donc  appartient à
appartient à  , ce qui montre l'inclusion
, ce qui montre l'inclusion 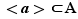 ; l'autre inclusion étant évidente, l'étape 1 est prouvée.
; l'autre inclusion étant évidente, l'étape 1 est prouvée.
Étape intermédiaire 2 : si l'ordre de  est fini, le théorème est vrai.
est fini, le théorème est vrai.
Preuve de l'étape 2. Notons  l'ordre de
l'ordre de  . Il découle du résultat de l'étape 1 que dans cette hypothèse l'ensemble
. Il découle du résultat de l'étape 1 que dans cette hypothèse l'ensemble 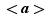 possède au plus
possède au plus  éléments. L'étudiant distrait croira même qu'on a déjà prouvé qu'il en possède exactement
éléments. L'étudiant distrait croira même qu'on a déjà prouvé qu'il en possède exactement  et qu'on a donc fini, mais son condisciple plus observateur remarquera que nous ne savons pas encore si dans l'énumération
et qu'on a donc fini, mais son condisciple plus observateur remarquera que nous ne savons pas encore si dans l'énumération 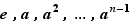 figurent bien
figurent bien  éléments distincts.
éléments distincts.
Prouvons donc ce dernier fait ; supposons que dans cette énumération il y ait deux termes 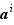 et
et 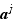 qui représentent le même élément du groupe, avec pourtant
qui représentent le même élément du groupe, avec pourtant  . On aurait alors
. On aurait alors 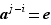 . Mais par ailleurs, comme
. Mais par ailleurs, comme  , on obtient
, on obtient 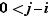 et donc
et donc 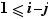 , et comme
, et comme  et
et 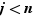 , on obtient
, on obtient  . Mais ceci contredit la définition de
. Mais ceci contredit la définition de  comme le plus petit entier supérieur ou égal à
comme le plus petit entier supérieur ou égal à  tel que
tel que 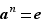 . L'hypothèse était donc absurde, et l'énumération décrivant
. L'hypothèse était donc absurde, et l'énumération décrivant 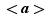 à l'étape 1 est une énumération sans répétition.
à l'étape 1 est une énumération sans répétition.
Le nombre d'éléments de 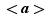 est donc bien égal à
est donc bien égal à  , et l'étape 1 est prouvée.
, et l'étape 1 est prouvée.
Étape intermédiaire 3 : si l'ordre de  est infini, le théorème est vrai.
est infini, le théorème est vrai.
Preuve de l'étape 3. Dans ce cas, tout le travail consiste à prouver que 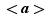 est un ensemble infini. La vérification est du même esprit qu'à l'étape 2, en plus simple : on va prouver que pour
est un ensemble infini. La vérification est du même esprit qu'à l'étape 2, en plus simple : on va prouver que pour  , les éléments
, les éléments 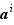 et
et 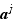 de
de 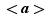 sont distincts. Pour ce faire, supposons que deux d'entre eux soient égaux ; on aurait alors
sont distincts. Pour ce faire, supposons que deux d'entre eux soient égaux ; on aurait alors 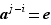 , avec pourtant
, avec pourtant 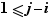 et
et  ne serait pas d'ordre infini. Ainsi l'étape 3 est prouvée.
ne serait pas d'ordre infini. Ainsi l'étape 3 est prouvée.
Corollaire  L'ordre d'un élément divise l'ordre du groupe.
L'ordre d'un élément divise l'ordre du groupe.
Laissée au lecteur, en lui rappelant l'existence dans ce cours d'un théorème dit «de Lagrange» et en lui conseillant tout de même de bien distinguer entre ordre (cardinal) et ordre (d'un élément), comme déjà mentionné.
Histoire d'utiliser encore un peu la notion d'ordre, donnons un énoncé qui peut servir pour gagner du temps dans tel ou tel exercice très concret.
Proposition  Soit
Soit  un groupe fini et
un groupe fini et  un sous-ensemble de
un sous-ensemble de  . Alors
. Alors  est un sous-groupe de
est un sous-groupe de  si et seulement si :
si et seulement si :
1. L'ensemble  n'est pas vide.
n'est pas vide.
2. Pour tous  de
de  , le produit
, le produit  est aussi dans
est aussi dans  .
.
En d'autres termes, dans le cas particulier d'un sous-ensemble d'un groupe fini (et seulement dans ce cas !) on peut faire des économies et éviter de travailler sur les ennuyeux symétriques pour examiner un potentiel sous-groupe.
Pour enfoncer le clou sur la nécessité de l'hypothèse selon laquelle  est fini, on pensera au cas
est fini, on pensera au cas 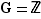 et
et 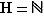 .
.
La seule difficulté est évidemment de vérifier la propriété (iii) de la définition des «sous-groupes». Prenons donc un élément  de
de  . On commence par traiter à part le cas stupide où
. On commence par traiter à part le cas stupide où 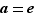 , et où il est clair qu'on a aussi
, et où il est clair qu'on a aussi  . Pour le cas sérieux où
. Pour le cas sérieux où  , considérons le sous-groupe
, considérons le sous-groupe 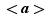 de
de  . Ce sous-groupe est fini, puisqu'inclus dans
. Ce sous-groupe est fini, puisqu'inclus dans  . On déduit donc du théorème précédent (en fait de sa partie la plus facile, l'étape 3 de sa preuve) que
. On déduit donc du théorème précédent (en fait de sa partie la plus facile, l'étape 3 de sa preuve) que  est d'ordre fini. Notons
est d'ordre fini. Notons  l'ordre de
l'ordre de  ; comme
; comme  , on a l'inégalité
, on a l'inégalité 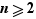 et donc
et donc 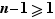 ; écrivons l'identité
; écrivons l'identité  , et revenons dans cette formule à la définition de
, et revenons dans cette formule à la définition de  : on obtient
: on obtient 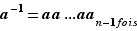 comme produit d'un nombre positif d'exemplaires de
comme produit d'un nombre positif d'exemplaires de  ; par la propriété 2 de l'énoncé de la proposition, on en déduit que
; par la propriété 2 de l'énoncé de la proposition, on en déduit que  .
.
9. Anneaux et corps
Il s'agit ici simplement de rajouter un peu de vocabulaire pour pouvoir décrire les propriétés que possèdent les ensembles de nombres usuels. Le chapitre se limitera donc à quelques définitions.
Définition 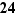 Soit
Soit  un ensemble muni de deux opérations, notées
un ensemble muni de deux opérations, notées 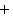 et
et  . On dit que
. On dit que  est un anneau lorsque les assertions (i) à (iv) sont vraies.
est un anneau lorsque les assertions (i) à (iv) sont vraies.
(i) Pour l'addition,  est un groupe commutatif.
est un groupe commutatif.
(ii) La multiplication est associative.
(iii) La multiplication possède un élément neutre.
(iv) La multiplication est distributive par rapport à l'addition ; en d'autres termes, pour tous  ,
,  et
et 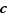 éléments de
éléments de  ,
, 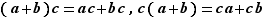
L'archétype de l'anneau est l'ensemble  des entiers relatifs ; dans un anneau quelconque on peut calculer «comme» dans
des entiers relatifs ; dans un anneau quelconque on peut calculer «comme» dans  . Méfiance sur un seul point toutefois : la définition n'exigeant pas que la multiplication soit commutative, certaines formules peuvent être un peu plus perverses ; par exemple
. Méfiance sur un seul point toutefois : la définition n'exigeant pas que la multiplication soit commutative, certaines formules peuvent être un peu plus perverses ; par exemple  se développe en
se développe en 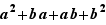 , mais ne peut pas dans un anneau trop général être regroupé en
, mais ne peut pas dans un anneau trop général être regroupé en 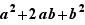 puisque
puisque 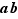 n'a aucune raison d'être égal à
n'a aucune raison d'être égal à  .
.
Voici un autre exemple.
Proposition 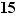 Soit
Soit  un espace vectoriel. L'ensemble des applications linéaires de
un espace vectoriel. L'ensemble des applications linéaires de  vers
vers  , noté
, noté 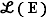 , est un anneau pour l'addition et la composition.
, est un anneau pour l'addition et la composition.
Les propriétés d'«anneau» sont généralement évidentes à vérifier ; la plus intéressante est la distributivité, qui est liée à la linéarité, et que nous laissons gentiment au lecteur. Le neutre pour la composition est sans surprise l'application identique.
Si on choisit pour espace vectoriel 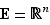 et que l'on représente les éléments de
et que l'on représente les éléments de 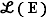 par des matrices carrées, on obtient l'anneau
par des matrices carrées, on obtient l'anneau 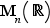 des matrices carrées de taille
des matrices carrées de taille 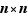 à coefficients réels.
à coefficients réels.
Définition 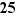 Soit
Soit  un anneau et
un anneau et 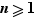 un entier. L'anneau des matrices carrées de taille
un entier. L'anneau des matrices carrées de taille  à coefficients dans
à coefficients dans  , noté
, noté 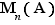 , est défini par les lois de composition suivantes. Si
, est défini par les lois de composition suivantes. Si 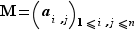 et
et 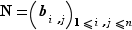 sont deux éléments de
sont deux éléments de 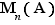 ,
, 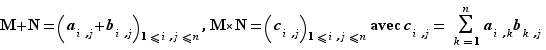
Le neutre de 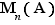 pour l'addition est la matrice nulle, dont tous les coefficients valent le neutre de l'addition de
pour l'addition est la matrice nulle, dont tous les coefficients valent le neutre de l'addition de  . Le neutre de
. Le neutre de 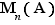 pour la multiplication est la matrice identité, dont tous les coefficients valent le neutre de l'addition de
pour la multiplication est la matrice identité, dont tous les coefficients valent le neutre de l'addition de  sauf ceux de la diagonale qui valent le neutre de la multiplication de
sauf ceux de la diagonale qui valent le neutre de la multiplication de  .
.
Définition  Un anneau est dit commutatif quand sa multiplication est commutative.
Un anneau est dit commutatif quand sa multiplication est commutative.
Définition 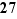 Un anneau
Un anneau  est dit intègre lorsque :
est dit intègre lorsque :
(i) L'anneau  possède au moins deux éléments.
possède au moins deux éléments.
(ii) Pour tous  et
et  éléments non nuls de
éléments non nuls de  ,
, 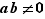 .
.
Une classe particulière d'anneaux est celle des anneaux tels que la deuxième loi (la multiplication) fournit aussi une structure de groupe (sur l'anneau privé de son zéro).
Définition  On dit qu'un anneau
On dit qu'un anneau 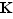 est un corps commutatif lorsque :
est un corps commutatif lorsque :
(i) La multiplication est commutative.
(ii) L'anneau 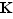 possède au moins deux éléments.
possède au moins deux éléments.
(iii) Tout élément non nul de 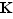 possède un inverse pour la multiplication.
possède un inverse pour la multiplication.
Les archétypes de corps commutatifs sont naturellement  , ensemble des fractions, et, encore mieux connus des étudiants,
, ensemble des fractions, et, encore mieux connus des étudiants,  et
et  . Un autre archétype, au moins aussi important malgré sa simplicité, est
. Un autre archétype, au moins aussi important malgré sa simplicité, est 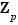 pour
pour 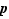 premier. Nous avons déjà défini l'addition sur
premier. Nous avons déjà défini l'addition sur 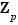 . On définit une multiplication
. On définit une multiplication  , en convenant que
, en convenant que  est l'unique entier
est l'unique entier 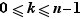 tel que
tel que 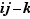 est divisible par
est divisible par  . On démontre facilement que
. On démontre facilement que 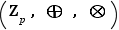 est un anneau pour tout entier
est un anneau pour tout entier 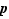 , et que c'est un corps, si et seulement si
, et que c'est un corps, si et seulement si 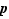 est premier. Ces corps servent entre autres en cryptographie. Le plus petit d'entre eux,
est premier. Ces corps servent entre autres en cryptographie. Le plus petit d'entre eux, 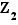 , peut être considéré comme la base de toute l'informatique : excusez du peu !
, peut être considéré comme la base de toute l'informatique : excusez du peu !