Site http://www.epsilon-publi.net/
- espace http://www.epsilon-publi.net/b/bycart/ de B. Ycart, professeur de mathématique, Université Joseph-Fourier
|
Pour visualiser le document avec epsilonwriter, cliquer ici |
Dérivabilité et convexité
Bernard Ycart
Sommaire
D'accord, vous n'avez pas attendu ce chapitre pour dériver des fonctions. Attention cependant à deux nouveautés importantes : le théorème des accroissements finis et la convexité. Une bonne maîtrise de la notion de limite vous sera indispensable pour tout comprendre.
1. Taux d'accroissement et dérivée
On considère une fonction  , de
, de  dans
dans  , définie sur un intervalle ouvert
, définie sur un intervalle ouvert  . Soit
. Soit  un point de
un point de  .
.
Définition 1 On appelle taux d'accroissement de  en
en  , la fonction
, la fonction 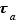 suivante.
suivante.
 |
 |
|
 |
 |
 |
 |
 |
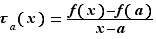 |
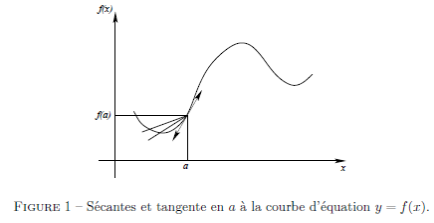
Si 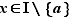 , la valeur de
, la valeur de 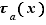 est le rapport de l'accroissement de la fonction,
est le rapport de l'accroissement de la fonction, 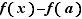 , à l'accroissement de la variable
, à l'accroissement de la variable 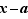 . Sur le graphe de la fonction, c'est la pente de la droite passant par les points du graphe
. Sur le graphe de la fonction, c'est la pente de la droite passant par les points du graphe 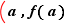 et
et 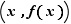 . Cette droite s'appelle une sécante. Si
. Cette droite s'appelle une sécante. Si  est un intervalle de temps et
est un intervalle de temps et 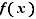 désigne la position d'un point mobile au temps
désigne la position d'un point mobile au temps  ,
, 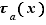 est la vitesse moyenne du mobile sur l'intervalle
est la vitesse moyenne du mobile sur l'intervalle ![[a,x]](_derivees.html/image19.png) (distance parcourue divisée par le temps de parcours).
(distance parcourue divisée par le temps de parcours).
Définition 2 On dit que  est dérivable en
est dérivable en  si le taux d'accroissement
si le taux d'accroissement 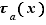 converge, quand
converge, quand  tend vers
tend vers  . Si c'est le cas, sa limite est la dérivée de
. Si c'est le cas, sa limite est la dérivée de  en
en  et se note
et se note 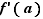 .
. 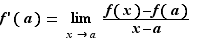 La dérivée de
La dérivée de  est la fonction
est la fonction 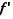 , qui à un point associe la dérivée de
, qui à un point associe la dérivée de  en ce point, si elle existe.
en ce point, si elle existe.
Géométriquement, la valeur de la dérivée en  est la pente de la tangente en
est la pente de la tangente en  à la courbe d'équation
à la courbe d'équation 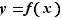 (figure 1). Si
(figure 1). Si 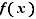 est la position d'un mobile à l'instant
est la position d'un mobile à l'instant  ,
, 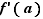 est sa vitesse instantanée à l'instant
est sa vitesse instantanée à l'instant  .
.
Voici deux cas particuliers.
 Si
Si  est constante, ses taux d'accroissements sont nuls, et donc sa dérivée en tout point est nulle.
est constante, ses taux d'accroissements sont nuls, et donc sa dérivée en tout point est nulle. 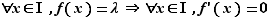
 Si
Si  est linéaire, ses taux d'accroissements sont constants, et donc sa dérivée en tout point est constante.
est linéaire, ses taux d'accroissements sont constants, et donc sa dérivée en tout point est constante. 
Il est souvent commode de se ramener à des limites en  , en écrivant :
, en écrivant : 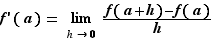
Voici une écriture équivalente.
Proposition 1 La fonction  admet
admet 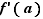 comme dérivée en
comme dérivée en  si et seulement si, au voisinage de
si et seulement si, au voisinage de  pour
pour 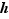 :
: 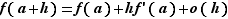
Le taux d'accroissement 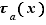 admet
admet 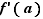 pour limite en
pour limite en  si et seulement si :
si et seulement si : 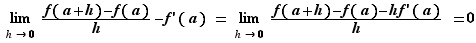
Par définition, ceci équivaut à dire que 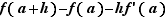 est négligeable devant
est négligeable devant 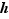 , au voisinage de
, au voisinage de  :
: 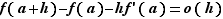
Définition 3 On dit que la fonction  admet un développement limité d'ordre 1 en
admet un développement limité d'ordre 1 en  si :
si : 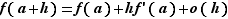
Dire que  admet un développement limité d'ordre
admet un développement limité d'ordre 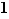 au voisinage de
au voisinage de  , c'est donner une approximation : on affirme par là que, si
, c'est donner une approximation : on affirme par là que, si 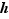 est petit,
est petit, 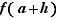 peut être approché par la valeur de
peut être approché par la valeur de  en
en  ,
, 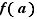 , plus un terme linéaire
, plus un terme linéaire 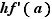 . La différence entre
. La différence entre 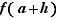 et cette approximation est négligeable devant
et cette approximation est négligeable devant 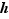 .
.
Si  est dérivable en
est dérivable en  , elle est nécessairement continue en ce point.
, elle est nécessairement continue en ce point.
Proposition 2 Si  est dérivable en
est dérivable en  , alors
, alors  est continue en
est continue en  .
.
Écrivons le développement limité d'ordre 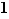 :
: 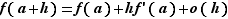 On en déduit
On en déduit 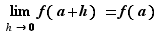 ce qui équivaut à :
ce qui équivaut à : 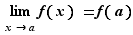
Voici un premier exemple.
Proposition 3 Soit 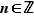 un entier fixé. La fonction
un entier fixé. La fonction 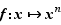 est dérivable en tout point
est dérivable en tout point  où elle est définie, et :
où elle est définie, et : 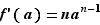
Si 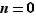 la fonction est constante et sa dérivée est nulle. Supposons
la fonction est constante et sa dérivée est nulle. Supposons 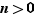 . Écrivons le taux d'accroissement de
. Écrivons le taux d'accroissement de  en
en  . Pour
. Pour 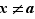 :
: 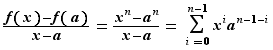 La somme contient
La somme contient 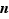 termes, dont chacun tend vers
termes, dont chacun tend vers 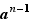 quand
quand  tend vers
tend vers  .
.
Considérons maintenant la fonction 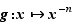 , définie pour
, définie pour 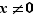 . Son taux d'accroissement en
. Son taux d'accroissement en 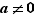 s'écrit :
s'écrit :
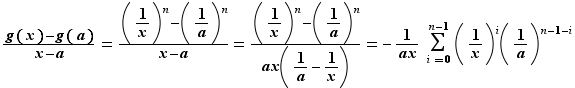
La somme contient 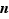 termes, dont chacun tend vers
termes, dont chacun tend vers 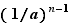 quand
quand  tend vers
tend vers  . Le taux d'accroissement a donc pour limite
. Le taux d'accroissement a donc pour limite 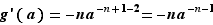
Prenons par exemple 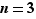 et
et  . On obtient :
. On obtient : 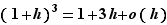 L'expression exacte est :
L'expression exacte est : 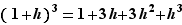 Si
Si 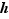 est petit (pensez
est petit (pensez 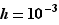 ), la valeur approchée
), la valeur approchée 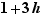 est effectivement très proche de la valeur exacte
est effectivement très proche de la valeur exacte 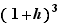 .
.
Il peut se faire que le taux d'accroissement admette seulement une limite unilatérale en  , auquel cas on parle de dérivée à gauche ou de dérivée à droite.
, auquel cas on parle de dérivée à gauche ou de dérivée à droite.
Définition 4 On dit que  est dérivable à gauche (respectivement : dérivable à droite) en
est dérivable à gauche (respectivement : dérivable à droite) en  si le taux d'accroissement
si le taux d'accroissement 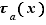 admet une limite à gauche (respectivement : à droite) en
admet une limite à gauche (respectivement : à droite) en  . Si c'est le cas, sa limite est la dérivée à gauche de
. Si c'est le cas, sa limite est la dérivée à gauche de  en
en  (respectivement : dérivée à droite de
(respectivement : dérivée à droite de  en
en  ).
).
Considérons par exemple la fonction valeur absolue 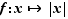 . Son taux d'accroissement en
. Son taux d'accroissement en  est :
est : 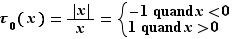
La fonction  n'est donc pas dérivable en
n'est donc pas dérivable en  , mais elle admet une dérivée à gauche égale à
, mais elle admet une dérivée à gauche égale à 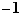 , et une dérivée à droite égale à
, et une dérivée à droite égale à 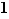 .
.
Il se peut aussi que la fonction ne soit définie que sur un intervalle dont  est une borne, auquel cas, on ne peut espérer qu'une dérivée unilatérale. Considérons la fonction suivante.
est une borne, auquel cas, on ne peut espérer qu'une dérivée unilatérale. Considérons la fonction suivante.
 |
 |
|
![]-∞,1]](_derivees.html/image66.png) |
 |
 |
 |
 |
 |
Son taux d'accroissement en  est défini, pour
est défini, pour ![x∈]-∞,1]](_derivees.html/image68.png) , par
, par 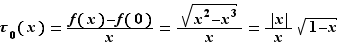 et donc :
et donc : 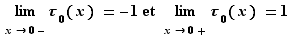 La fonction
La fonction  admet une dérivée à gauche et une dérivée à droite en
admet une dérivée à gauche et une dérivée à droite en  , mais elles sont différentes :
, mais elles sont différentes :  n'est pas dérivable en
n'est pas dérivable en  .
.
Considérons maintenant le taux d'accroissement en 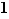 . Pour
. Pour 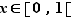 , il vaut :
, il vaut : 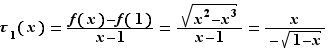 et donc :
et donc : 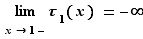 La fonction
La fonction  n'admet pas de dérivée à gauche en
n'admet pas de dérivée à gauche en 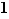 . Le fait que la limite du taux d'accroissement soit
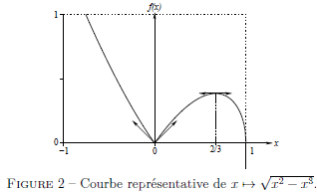
. Le fait que la limite du taux d'accroissement soit 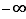 se traduit par une tangente verticale à la courbe représentative (figure 2).
se traduit par une tangente verticale à la courbe représentative (figure 2).
2. Opérations sur les dérivées
Les résultats de cette section sont à connaître par cœur : ils vous permettent de calculer les dérivées de toutes les fonctions que vous rencontrerez, à partir d'un petit nombre de dérivées usuelles.
Théorème 1 Soient  et
et 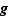 deux fonctions définies sur un intervalle
deux fonctions définies sur un intervalle  contenant
contenant  . On suppose que
. On suppose que  et
et 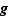 sont dérivables en
sont dérivables en  . Alors :
. Alors :
 est dérivable en
est dérivable en  , de dérivée
, de dérivée 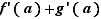
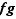 est dérivable en
est dérivable en  , de dérivée
, de dérivée  .
.
Comme cas particulier du point 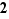 , si
, si 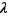 est une constante, la dérivée de
est une constante, la dérivée de 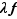 est
est 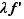 . Par hypothèse,
. Par hypothèse, 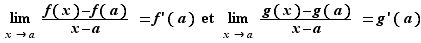
Écrivons le taux d'accroissement de la somme. 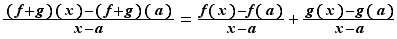 Comme la limite de la somme est la somme des limites, le résultat s'ensuit.
Comme la limite de la somme est la somme des limites, le résultat s'ensuit.
Écrivons le taux d'accroissement du produit.  Comme
Comme 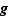 est dérivable, elle est continue en
est dérivable, elle est continue en  , donc
, donc 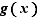 tend vers
tend vers  quand
quand  tend vers
tend vers  . La limite d'un produit est le produit des limites, idem pour la somme. D'où le résultat.
. La limite d'un produit est le produit des limites, idem pour la somme. D'où le résultat.
Le théorème 1, combiné avec la proposition 3, entraîne en particulier que toute fonction polynôme est dérivable sur  .
.
Théorème 2 Soit  une fonction définie sur un intervalle ouvert
une fonction définie sur un intervalle ouvert  de
de  , dérivable en
, dérivable en  . Soit
. Soit 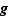 une fonction définie sur un intervalle ouvert contenant
une fonction définie sur un intervalle ouvert contenant 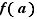 , dérivable en
, dérivable en 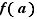 . Alors la composée
. Alors la composée 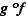 est dérivable en
est dérivable en  , de dérivée :
, de dérivée : 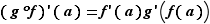
Par hypothèse, les taux d'accroissement de  en
en  et de
et de 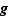 en
en 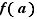 convergent :
convergent :  Nous allons utiliser en plus les conséquences suivantes :
Nous allons utiliser en plus les conséquences suivantes :
C1 :  est continue en
est continue en  ,
,
C2 : si 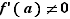 alors
alors 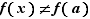 au voisinage de
au voisinage de  ,
,
C3 : le taux d'accroissement de 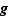 est borné au voisinage de
est borné au voisinage de 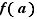 .
.
L'idée consiste à écrire le taux d'accroissement de 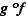 en
en  comme un produit de deux taux :
comme un produit de deux taux : 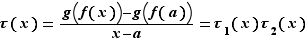 avec :
avec : 
Évidemment, 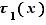 n'est défini que si
n'est défini que si 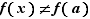 . Mais si
. Mais si 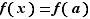 , alors
, alors 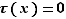 .
.
Considérons d'abord le cas où 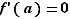 . Dans ce cas,
. Dans ce cas, 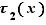 tend vers
tend vers  , et comme conséquence de C1 et C3, il existe un intervalle
, et comme conséquence de C1 et C3, il existe un intervalle  et une constante
et une constante  telle que :
telle que : 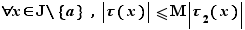 Donc
Donc 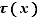 converge vers
converge vers  .
.
Considérons maintenant le cas où 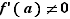 . Comme conséquence de C2,
. Comme conséquence de C2, 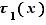 est bien défini au voisinage de
est bien défini au voisinage de  . La convergence de
. La convergence de 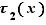 vers
vers 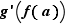 découle de la dérivabilité de
découle de la dérivabilité de 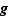 et de la continuité de
et de la continuité de  (composition des limites).
(composition des limites).
D'après la proposition 3, appliquée à la fonction inverse 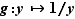 , celle-ci est dérivable en tout point
, celle-ci est dérivable en tout point  où elle est définie, et
où elle est définie, et  .
.
On déduit du théorème 2 que si  est dérivable et ne s'annule pas en
est dérivable et ne s'annule pas en  , alors son inverse
, alors son inverse 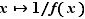 est dérivable, de dérivée
est dérivable, de dérivée 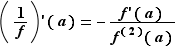
En combinant ceci avec la formule donnant la dérivée d'un produit, on obtient la dérivée d'un quotient. 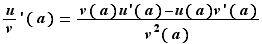
Attention à ne pas confondre l'inverse 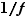 avec la fonction réciproque
avec la fonction réciproque 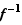 dans le cas où
dans le cas où  est bijective.
est bijective.
Proposition 4 Soit  une bijection d'un intervalle ouvert
une bijection d'un intervalle ouvert  vers un intervalle ouvert
vers un intervalle ouvert  . Soit
. Soit  un point de
un point de  et
et 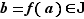 . Si
. Si  est dérivable en
est dérivable en  , de dérivée non nulle, alors la fonction réciproque
, de dérivée non nulle, alors la fonction réciproque 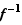 est dérivable en
est dérivable en  , et :
, et :
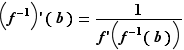
Pour tout point 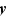 de
de  , il existe un unique
, il existe un unique 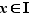 tel que
tel que 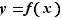 . Écrivons le taux d'accroissement de
. Écrivons le taux d'accroissement de 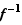 en
en  : pour tout
: pour tout 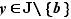 ,
,  Puisque
Puisque  est continue en
est continue en  ,
, 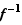 est continue en
est continue en  , et donc
, et donc 
Les théorèmes de cette section permettent de démontrer la dérivabilité de toutes les fonctions que vous aurez à examiner, à condition d'admettre la dérivabilité des «briques de base» que sont les fonctions usuelles.
Toutes les fonctions usuelles sont dérivables en tout point d'un intervalle ouvert où elles sont définies.
Ceci concerne les fonctions polynômes, fractions rationnelles, puissances, exponentielle, logarithme, sinus, cosinus, mais exclut bien sûr la valeur absolue.
Voici un tableau récapitulatif des formules de dérivation à connaître par cœur.
 |
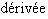 |
 |
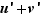 |
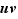 |
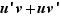 |
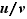 |
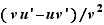 |
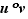 |
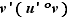 |
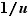 |
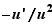 |
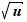 |
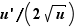 |
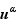 |
 |
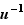 |
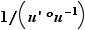 |
Les dérivées suivantes doivent être connues.
 |
 |
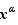 |
 |
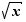 |
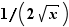 |
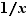 |
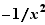 |
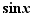 |
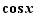 |
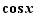 |
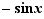 |
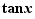 |
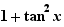 |
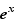 |
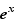 |
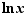 |
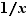 |
La connaissance des dérivées usuelles, permet, en appliquant la définition def:derivee, de calculer des limites de taux d'accroissement. À titre d'exemple, nous donnons ci-dessous trois limites à connaître.
Théorème 3 Au voisinage de  ,
, 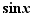 ,
, 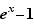 et
et 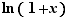 sont équivalents à
sont équivalents à  .
.
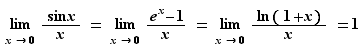
Les trois limites sont démontrées dans l'ordre.
La dérivée de la fonction sinus en  est
est  . Son taux d'accroissement en
. Son taux d'accroissement en  est :
est : 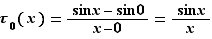 D'où le résultat.
D'où le résultat.
La dérivée de la fonction exponentielle en  est
est  . Son taux d'accroissement en
. Son taux d'accroissement en  est :
est : 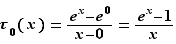 D'où le résultat.
D'où le résultat.
La dérivée de la fonction 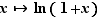 en
en  est
est 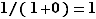 . Son taux d'accroissement en
. Son taux d'accroissement en  est :
est :  D'où le résultat.
D'où le résultat.
3. Dérivées successives
Etant donné un intervalle ouvert  , on dit que
, on dit que  est dérivable sur
est dérivable sur  , si elle est dérivable en tout point de
, si elle est dérivable en tout point de  . Soit
. Soit  une fonction dérivable sur
une fonction dérivable sur  . Sa dérivée
. Sa dérivée 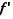 peut être elle-même dérivable. On appelle alors dérivée seconde la dérivée de
peut être elle-même dérivable. On appelle alors dérivée seconde la dérivée de 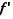 , et on la note
, et on la note 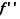 . Cette fonction peut être elle-même dérivable, etc. Si
. Cette fonction peut être elle-même dérivable, etc. Si  est
est 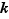 fois dérivable, on note
fois dérivable, on note  sa dérivée d'ordre
sa dérivée d'ordre 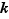 , ou dérivée
, ou dérivée 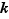 -ième. Par définition, la dérivée d'ordre
-ième. Par définition, la dérivée d'ordre  est la fonction elle-même.
est la fonction elle-même.
Par exemple, si 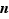 est un entier fixé, et
est un entier fixé, et  est la fonction
est la fonction 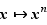 ,
, 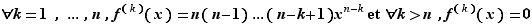 Vous rencontrerez souvent les notations suivantes, que nous n'utiliserons pas ici.
Vous rencontrerez souvent les notations suivantes, que nous n'utiliserons pas ici.
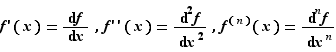
Définition 5 Soit  une fonction définie sur un intervalle
une fonction définie sur un intervalle  de
de  . On dit que
. On dit que  est de classe
est de classe 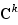 sur
sur  , ou encore
, ou encore  est
est 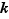 fois continûment dérivable, si elle admet une dérivée
fois continûment dérivable, si elle admet une dérivée 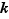 -ième continue sur
-ième continue sur  .
.
On dit que  est de classe
est de classe 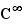 sur
sur  , si elle admet des dérivées successives de tout ordre (elles sont nécessairement continues puisque dérivables). Vous pouvez retenir que :
, si elle admet des dérivées successives de tout ordre (elles sont nécessairement continues puisque dérivables). Vous pouvez retenir que :
toutes les fonctions usuelles sont de classe 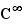 sur les intervalles ouverts où elles sont définies.
sur les intervalles ouverts où elles sont définies.
Ceci concerne les fonctions polynômes, fractions rationnelles, puissances, exponentielle, logarithme, sinus, cosinus.
La formule de Leibniz, très proche de la formule du binôme de Newton, exprime la dérivée 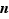 -ième d'un produit à d'aide des dérivées successives des composantes.
-ième d'un produit à d'aide des dérivées successives des composantes.
Proposition 5 Si  et
et 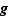 sont deux fonctions de
sont deux fonctions de  dans
dans  ,
, 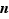 fois dérivables sur un intervalle
fois dérivables sur un intervalle  , alors le produit
, alors le produit 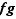 est
est 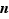 fois dérivable sur
fois dérivable sur  et :
et :
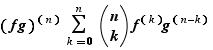
par récurrence sur 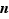 . Puisque par définition
. Puisque par définition 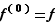 , la formule est vraie pour
, la formule est vraie pour 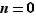 . Supposons qu'elle est vraie pour
. Supposons qu'elle est vraie pour 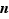 . Si
. Si  et
et 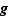 sont dérivables
sont dérivables 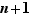 fois sur
fois sur  , alors pour tout
, alors pour tout 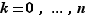 , le produit
, le produit 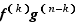 est dérivable et sa dérivée est :
est dérivable et sa dérivée est : 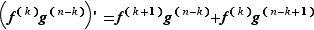 D'après (leibniz),
D'après (leibniz),  est dérivable, comme combinaison linéaire de fonctions dérivables. Sa dérivée s'écrit :
est dérivable, comme combinaison linéaire de fonctions dérivables. Sa dérivée s'écrit :
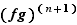 |
 |
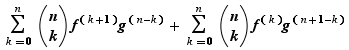 |
 |
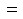 |
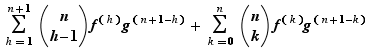 |
 |
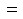 |
 |
 |
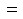 |
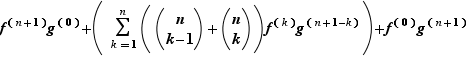 |
 |
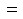 |
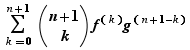 |
Pour la dernière égalité, nous avons appliqué la formule du triangle de Pascal. La formule est vraie pour 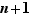 , donc pour tout
, donc pour tout 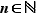 , par récurrence.
, par récurrence.
À titre d'exemple, calculons la dérivée 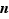 -ième de
-ième de 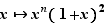 . Posons
. Posons 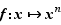 et
et  . Alors :
. Alors : 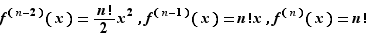 et
et 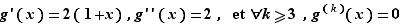 Par application de 1,
Par application de 1, 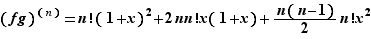
4. Théorème des accroissements finis
En un point où la dérivée d'une fonction s'annule, les accroissements de la fonction sont négligeables devant les accroissements de la variable. Souvent, c'est un point où les variations de la fonction changent de sens, donc un maximum ou un minimum.
Définition 6 Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle ouvert
, définie sur un intervalle ouvert  . Soit
. Soit  un point de
un point de  . On dit que
. On dit que  est un
est un
 maximum local de
maximum local de  si
si 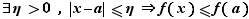
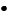 minimum local de
minimum local de  si
si 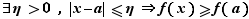
Insistons sur l'adjectif local. Il suffit que la valeur de  en
en  soit la plus grande des valeurs prises par
soit la plus grande des valeurs prises par  sur un petit intervalle autour de
sur un petit intervalle autour de  pour que
pour que  soit un maximum local. Cette valeur n'est pas nécessairement la plus grande prise par
soit un maximum local. Cette valeur n'est pas nécessairement la plus grande prise par  sur tout son domaine de définition (voir le graphe de la figure 3).
sur tout son domaine de définition (voir le graphe de la figure 3).
Théorème 4 Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle ouvert
, définie sur un intervalle ouvert  . Si
. Si  présente un extremum (maximum ou minimum) local en un point
présente un extremum (maximum ou minimum) local en un point  de
de  , et si
, et si  est dérivable en
est dérivable en  , alors
, alors 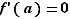 .
.
Si  est un minimum local de
est un minimum local de  , alors c'est un maximum local de
, alors c'est un maximum local de 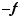 : quitte à remplacer
: quitte à remplacer  par
par 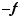 , nous pouvons supposer que
, nous pouvons supposer que  est un maximum local.
est un maximum local. 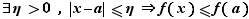 Donc pour tout
Donc pour tout  dans l'intervalle
dans l'intervalle 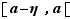 ,
,
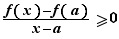 donc
donc 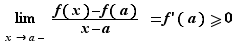
Pour tout  dans l'intervalle
dans l'intervalle ![]a,a+η[](_derivees.html/image198.png) ,
,
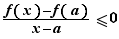 donc
donc 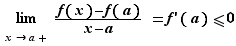
D'où le résultat.
Reprenons l'exemple de la figure fig:tanhorver :  . La dérivée est :
. La dérivée est :  Elle s'annule en
Elle s'annule en 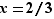 , et
, et  admet effectivement un maximum en ce point. Mais savoir que
admet effectivement un maximum en ce point. Mais savoir que 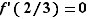 permet seulement d'affirmer que la tangente en ce point est horizontale. Il se pourrait que la dérivée en un point soit nulle sans que la fonction admette un extremum en ce point : par exemple la fonction
permet seulement d'affirmer que la tangente en ce point est horizontale. Il se pourrait que la dérivée en un point soit nulle sans que la fonction admette un extremum en ce point : par exemple la fonction 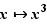 en
en  . D'autre part, une fonction peut présenter un extremum en
. D'autre part, une fonction peut présenter un extremum en  , sans être dérivable en ce point (par exemple la fonction
, sans être dérivable en ce point (par exemple la fonction  en
en  ).
).
Voici un autre exemple (figure 3). Soit  la fonction définie par :
la fonction définie par :
 |
 |
|
 |
 |
 |
 |
 |
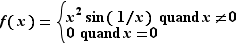 |
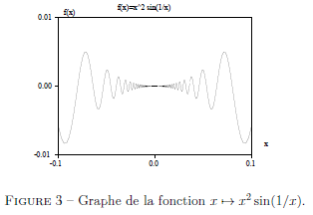
Le taux d'accroissement de  en
en  est
est 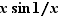 , qui tend vers
, qui tend vers  . La dérivée de
. La dérivée de  en
en  est donc nulle. Pourtant, tout intervalle contenant
est donc nulle. Pourtant, tout intervalle contenant  , contient aussi des valeurs positives, et des valeurs négatives (et aussi une infinité d'extrema locaux).
, contient aussi des valeurs positives, et des valeurs négatives (et aussi une infinité d'extrema locaux).
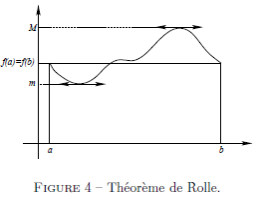
Nous allons appliquer le théorème 4, pour démontrer le théorème de Rolle.
Théorème 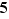 Soient
Soient  et
et  deux réels tels que
deux réels tels que 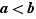 . Soit
. Soit  une fonction de
une fonction de ![[a,b]](_derivees.html/image213.png) dans
dans  , continue sur
, continue sur ![[a,b]](_derivees.html/image213.png) , dérivable sur
, dérivable sur ![]a,b[](_derivees.html/image214.png) . Si
. Si 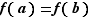 , alors la dérivée de
, alors la dérivée de  s'annule sur
s'annule sur ![]a,b[](_derivees.html/image214.png) .
.
![∃c∈]a,b[,f'(c)=0](_derivees.html/image216.png)
Une application continue sur intervalle fermé borné, atteint sa borne inférieure 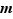 et sa borne supérieure
et sa borne supérieure 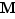 : il existe
: il existe ![c_1,c_2∈[a,b]](_derivees.html/image218.png) tels que pour tout
tels que pour tout ![x∈[a,b]](_derivees.html/image219.png) ,
, 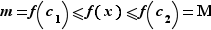 Si
Si 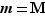 , l'application
, l'application  est constante sur
est constante sur ![[a,b]](_derivees.html/image213.png) , et sa dérivée est identiquement nulle. Si
, et sa dérivée est identiquement nulle. Si  , alors l'une au moins de ces deux valeurs est différente de
, alors l'une au moins de ces deux valeurs est différente de 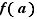 (et donc de
(et donc de  ). Si
). Si 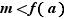 , alors
, alors ![c_1∈]a,b[](_derivees.html/image225.png) est un minimum pour
est un minimum pour  , et donc
, et donc  , d'après le théorème précédent. Si
, d'après le théorème précédent. Si  , alors
, alors 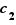 est un maximum pour
est un maximum pour  , et donc
, et donc 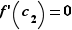 .
.
On en déduit le résultat le plus important de cette section, le théorème des accroissements finis.
Théorème 6 Soient  et
et  deux réels tels que
deux réels tels que  . Soit
. Soit  une fonction de
une fonction de ![[a,b]](_derivees.html/image213.png) dans
dans  , continue sur
, continue sur ![[a,b]](_derivees.html/image213.png) , dérivable sur
, dérivable sur ![]a,b[](_derivees.html/image214.png) .
.
![∃c∈]a,b[,(f(b)-f(a))/(b-...](_derivees.html/image232.png)
Considérons la fonction  , qui à
, qui à ![x∈[a,b]](_derivees.html/image219.png) associe
associe 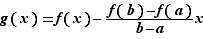 La fonction
La fonction 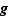 est continue sur
est continue sur ![[a,b]](_derivees.html/image213.png) , dérivable sur
, dérivable sur ![]a,b[](_derivees.html/image214.png) . De plus, elle prend la même valeur en
. De plus, elle prend la même valeur en  et
et  :
: 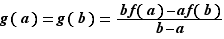 D'après le théorème de Rolle, la dérivée de
D'après le théorème de Rolle, la dérivée de 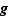 s'annule en un point
s'annule en un point 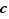 de
de ![]a,b[](_derivees.html/image214.png) .
. 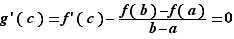 D'où le résultat.
D'où le résultat.
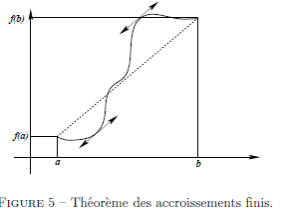
Graphiquement, le théorème des accroissements finis dit que la courbe représentative de  sur
sur ![[a,b]](_derivees.html/image213.png) possède au moins une tangente parallèle à la sécante passant par
possède au moins une tangente parallèle à la sécante passant par 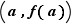 et
et 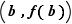 (figure 5). Si
(figure 5). Si 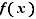 représente la position d'un mobile à l'instant
représente la position d'un mobile à l'instant  , le théorème des accroissements finis dit que en au moins un point, la vitesse instantanée doit être égale à la vitesse moyenne sur l'intervalle.
, le théorème des accroissements finis dit que en au moins un point, la vitesse instantanée doit être égale à la vitesse moyenne sur l'intervalle.
Le plus souvent en pratique, on ne sait rien de la valeur de 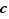 qui est telle que la tangente en
qui est telle que la tangente en 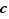 est parallèle à la sécante. Mais de son existence découlent des inégalités permettant d'obtenir des renseignements précis sur les accroissements de la fonction. Le théorème des accroissements finis permet aussi d'établir le lien entre le sens de variation de
est parallèle à la sécante. Mais de son existence découlent des inégalités permettant d'obtenir des renseignements précis sur les accroissements de la fonction. Le théorème des accroissements finis permet aussi d'établir le lien entre le sens de variation de  et le signe de sa dérivée.
et le signe de sa dérivée.
Proposition 6 Soit  un intervalle ouvert non vide, et
un intervalle ouvert non vide, et  une fonction dérivable sur
une fonction dérivable sur  . La fonction
. La fonction  est :
est :
 croissante sur
croissante sur  si et seulement si
si et seulement si 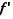 est positive ou nulle sur
est positive ou nulle sur  ,
,
 décroissante sur
décroissante sur  si et seulement si
si et seulement si 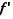 est négative ou nulle sur
est négative ou nulle sur  .
.
La fonction  est croissante si et seulement si
est croissante si et seulement si 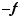 est décroissante. Il suffit donc de démontrer le premier point. Si
est décroissante. Il suffit donc de démontrer le premier point. Si  est croissante, alors ses taux d'accroissement sont tous positifs ou nuls :
est croissante, alors ses taux d'accroissement sont tous positifs ou nuls :  Comme la dérivée en chaque point est limite de taux d'accroissement, elle est aussi positive ou nulle.
Comme la dérivée en chaque point est limite de taux d'accroissement, elle est aussi positive ou nulle.
Réciproquement, soient  et
et 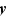 deux points de
deux points de  tels que
tels que 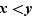 . Appliquons le théorème des accroissements finis à
. Appliquons le théorème des accroissements finis à  sur l'intervalle
sur l'intervalle ![[x,y]](_derivees.html/image241.png) : il existe
: il existe ![c∈]x,y[](_derivees.html/image242.png) tel que :
tel que : 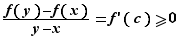 Donc
Donc 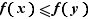 .
.
Ce résultat n'est valable que sur un intervalle : la fonction 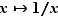 a une dérivée négative sur
a une dérivée négative sur 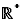 , pourtant elle n'est pas décroissante. D'autre part, si la dérivée est strictement positive, alors la fonction est strictement croissante. La réciproque est fausse. La fonction peut être strictement croissante même si la dérivée s'annule en certains points (par exemple
, pourtant elle n'est pas décroissante. D'autre part, si la dérivée est strictement positive, alors la fonction est strictement croissante. La réciproque est fausse. La fonction peut être strictement croissante même si la dérivée s'annule en certains points (par exemple 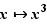 ).
).
Comme autre application du théorème des accroissements finis, il est possible d'obtenir la dérivée en un point comme prolongement par continuité de la dérivée calculée sur un intervalle.
Proposition 7 Soient  et
et  deux réels tels que
deux réels tels que 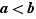 . Soit
. Soit  une fonction de
une fonction de  dans
dans  , continue sur l'intervalle
, continue sur l'intervalle ![[a,b]](_derivees.html/image213.png) , dérivable sur
, dérivable sur ![]a,b[](_derivees.html/image214.png) . Si
. Si 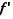 admet une limite finie en
admet une limite finie en  , alors
, alors  est dérivable à droite en
est dérivable à droite en  et :
et :
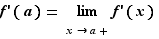
Soit ![x∈]a,b]](_derivees.html/image247.png) . Appliquons le théorème des accroissements finis sur l'intervalle
. Appliquons le théorème des accroissements finis sur l'intervalle ![[a,x]](_derivees.html/image19.png) . Il existe
. Il existe ![c∈]a,x[](_derivees.html/image248.png) tel que
tel que  Soit
Soit 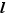 la limite à droite de
la limite à droite de 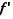 en
en  . Pour tout
. Pour tout 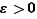 , il existe
, il existe 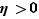 tel que
tel que 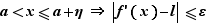 Donc pour
Donc pour 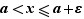 ,
, 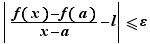 D'où le résultat.
D'où le résultat.
Ce résultat n'est qu'une condition suffisante. Il peut se faire que la dérivée existe sans qu'elle soit continue. Par exemple la fonction 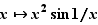 a une dérivée nulle en
a une dérivée nulle en  (figure 3). Pourtant sa dérivée en
(figure 3). Pourtant sa dérivée en  ,
, 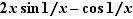 , n'a pas de limite en
, n'a pas de limite en  .
.
5. Fonctions convexes
Définition 7 Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle
, définie sur un intervalle  contenant au moins deux points. On dit que
contenant au moins deux points. On dit que  est convexe sur
est convexe sur  si et seulement si :
si et seulement si :
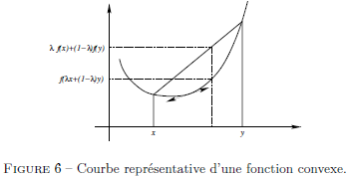
![∀ x,y∈I,∀ λ∈[0,1],f(λx+(...](_derivees.html/image258.png) (2)
(2)
Si 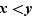 , et
, et ![λ∈[0,1]](_derivees.html/image259.png) , alors
, alors 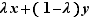 est un point de l'intervalle
est un point de l'intervalle ![[x,y]](_derivees.html/image241.png) . La condition
. La condition 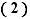 dit que le point de la courbe représentative d'abscisse
dit que le point de la courbe représentative d'abscisse 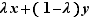 doit être situé au-dessous du segment de sécante joignant les points
doit être situé au-dessous du segment de sécante joignant les points 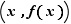 et
et 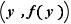 (figure 6). En d'autres termes, tout arc de la courbe représentative doit être situé au-dessous de sa corde. De manière équivalente, la partie du plan située au-dessus de la courbe représentative est une région convexe, au sens où tout segment joignant deux de ses points est entièrement contenu dans la région.
(figure 6). En d'autres termes, tout arc de la courbe représentative doit être situé au-dessous de sa corde. De manière équivalente, la partie du plan située au-dessus de la courbe représentative est une région convexe, au sens où tout segment joignant deux de ses points est entièrement contenu dans la région.
Une fonction est dite concave si son opposée est convexe. Les propriétés sont inversées : tout arc est au-dessus de sa corde. La région du plan située au-dessous de la courbe représentative est convexe.
La fonction exponentielle est convexe, la fonction logarithme est concave. La fonction 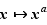 est convexe sur
est convexe sur 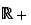 pour
pour  , elle est concave pour
, elle est concave pour  . La fonction
. La fonction 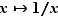 est convexe sur
est convexe sur 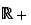 , concave sur
, concave sur 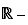 , de même que la fonction
, de même que la fonction 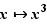 .
.
Voici une autre caractérisation de la convexité.
Proposition 8 prop:caracconvexe Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle
, définie sur un intervalle  contenant au moins deux points. La fonction
contenant au moins deux points. La fonction  est convexe sur
est convexe sur  si et seulement si, pour tout
si et seulement si, pour tout 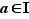 le taux d'accroissement
le taux d'accroissement 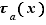 est une fonction croissante de
est une fonction croissante de  sur
sur 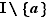 .
.
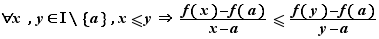
Commmençons par la condition nécessaire. Soit 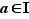 et
et 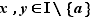 tels que
tels que 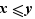 . Trois cas sont possibles :
. Trois cas sont possibles : 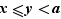 ,
, 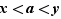 ,
, 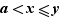 . Nous traitons le premier, les deux autres sont analogues. Soit
. Nous traitons le premier, les deux autres sont analogues. Soit 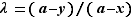 . Alors
. Alors  . Comme
. Comme  est convexe,
est convexe, 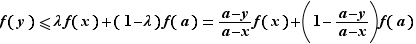 On en déduit :
On en déduit :  soit :
soit :  Montrons maintenant la condition suffisante. Soient
Montrons maintenant la condition suffisante. Soient  et
et 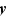 deux points de
deux points de  tels que
tels que 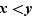 et
et 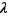 un réel dans
un réel dans ![[0,1]](_derivees.html/image281.png) . Posons
. Posons 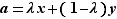 , et donc :
, et donc : 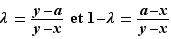 Si
Si 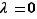 ou
ou 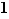 , l'inégalité est vérifiée. Nous pouvons donc supposer que
, l'inégalité est vérifiée. Nous pouvons donc supposer que  est différent de
est différent de  et
et 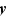 . Écrivons que le taux d'accroissement en
. Écrivons que le taux d'accroissement en  est croissant.
est croissant.  En multipliant les deux membres par le produit
En multipliant les deux membres par le produit 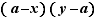 , qui est positif, on obtient :
, qui est positif, on obtient : 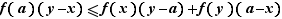 En divisant par
En divisant par 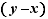 ceci donne :
ceci donne : 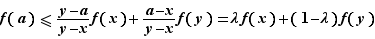
Corollaire 1 Si une fonction  est convexe sur un intervalle ouvert
est convexe sur un intervalle ouvert  , alors elle est dérivable à gauche et à droite en tout point de
, alors elle est dérivable à gauche et à droite en tout point de  , et donc continue sur
, et donc continue sur  .
.
Si 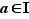 , le taux d'accroissement en
, le taux d'accroissement en  ,
, 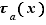 , est une fonction croissante de
, est une fonction croissante de  . Il admet donc en
. Il admet donc en  une limite à gauche et une limite à droite finies.
une limite à gauche et une limite à droite finies.
Ce résultat n'est pas valable si l'intervalle n'est pas ouvert. Par exemple la fonction qui vaut  sur
sur 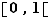 , et
, et 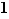 au point
au point 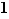 est convexe sur
est convexe sur ![[0,1]](_derivees.html/image281.png) , mais elle n'est pas continue en
, mais elle n'est pas continue en 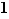 . Le fait qu'une dérivée à gauche et à droite existe, n'implique pas que la fonction soit dérivable. Par exemple, la fonction valeur absolue
. Le fait qu'une dérivée à gauche et à droite existe, n'implique pas que la fonction soit dérivable. Par exemple, la fonction valeur absolue  est convexe sur
est convexe sur  mais elle n'est pas dérivable en
mais elle n'est pas dérivable en  . Lorsque la fonction est dérivable, sa dérivée est croissante.
. Lorsque la fonction est dérivable, sa dérivée est croissante.
Proposition 9 Soit  une fonction de
une fonction de  dans
dans  , dérivable sur un intervalle ouvert
, dérivable sur un intervalle ouvert  . La fonction
. La fonction  est convexe sur
est convexe sur  si et seulement si sa dérivée
si et seulement si sa dérivée 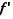 est croissante sur
est croissante sur  .
.
Commençons par la condition nécessaire. Soient  et
et 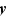 deux points de
deux points de  , tels que
, tels que 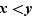 . Pour tout
. Pour tout ![z∈[x,y]](_derivees.html/image291.png) ,
, 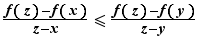 En faisant tendre
En faisant tendre  vers
vers  , on en déduit :
, on en déduit : 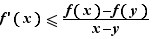 De même, en faisant tendre
De même, en faisant tendre 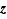 vers
vers 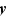 ,
, 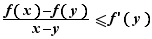 Donc
Donc 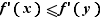 .
.
Montrons maintenant la condition suffisante. Soient  deux points de
deux points de  tels que
tels que 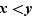 ,
, ![λ∈]0,1[](_derivees.html/image298.png) , et
, et 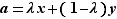 . Appliquons le théorème des accroissements finis sur les deux intervalles
. Appliquons le théorème des accroissements finis sur les deux intervalles ![[x,a]](_derivees.html/image299.png) et
et ![[a,y]](_derivees.html/image300.png) . Il existe
. Il existe ![c_1∈]x,a[](_derivees.html/image301.png) et
et ![c_2∈]a,y[](_derivees.html/image302.png) tels que :
tels que : 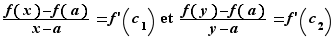 La fonction
La fonction 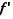 étant croissante, on a donc :
étant croissante, on a donc :  Comme nous l'avons déjà vu dans la démonstration de la proposition prop:caracconvexe, ceci entraîne
Comme nous l'avons déjà vu dans la démonstration de la proposition prop:caracconvexe, ceci entraîne 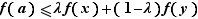
Graphiquement, la pente de la tangente d'une fonction convexe est croissante. Dans la démonstration précédente, nous avons établi les inégalités : 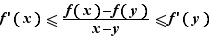 On en déduit que pour
On en déduit que pour 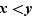 ,
, 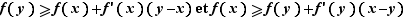 Donc la courbe représentative de
Donc la courbe représentative de  reste au-dessus de ses tangentes (figure fig:convexe).
reste au-dessus de ses tangentes (figure fig:convexe).
Corollaire 2 Soit  une fonction de
une fonction de  dans
dans  , deux fois dérivable sur un intervalle ouvert
, deux fois dérivable sur un intervalle ouvert  . La fonction
. La fonction  est convexe sur
est convexe sur  si et seulement si sa dérivée seconde
si et seulement si sa dérivée seconde 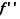 est positive ou nulle sur
est positive ou nulle sur  .
.
Une fonction deux fois dérivable est concave si et seulement si sa dérivée seconde est négative ou nulle. Les points où la dérivée seconde s'annule et change de signe correspondent graphiquement à des points où la courbe représentative passe de concave à convexe où inversement. On les appelle des points d'inflexion.