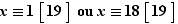Site http://www.epsilon-publi.net/
- espace http://www.epsilon-publi.net/b/bycart/ de B. Ycart, professeur de mathématique, Université Joseph-Fourier
|
Pour visualiser le document avec epsilonwriter, cliquer ici |
Arithmétique
Bernard Ycart
Licence CC-BY
Origine : M@ths en ligne - Université Joseph Fourier
Document produit en ouvrant un fichier Tex
Mots-clés: nombre premier, division euclidienne, PGCD, PPCM, facteurs premiers, sous-groupe, congruence
Sommaire
Guère d'introduction tonitruante à faire, sinon pour souligner que ce chapitre a le charme de n'utiliser comme notions admises que les notations de la théorie des ensembles naïve et les connaissances évidentes sur les entiers, et qu'il présente donc l'agrément de donner une image de démonstrations (que l'on espère) totalement crédibles.
1. Nombres premiers
On appelle entier (ou entier relatif, c'est-à-dire positif ou négatif) tout élément de
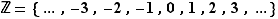
Définition On dit qu'un entier  est un multiple d'un entier
est un multiple d'un entier  , ou que
, ou que  est un diviseur de
est un diviseur de  lorsqu'il existe un entier
lorsqu'il existe un entier 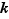 tel que
tel que 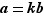 .
.
Définition On dit qu'un entier 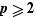 est premier lorsqu'il possède pour seuls diviseurs positifs
est premier lorsqu'il possède pour seuls diviseurs positifs 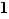 et lui-même.
et lui-même.
On notera au passage qu'au hasard des définitions, on parlera parfois d'entiers relatifs (les éléments de 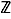 ) et parfois d'entiers naturels (les éléments de
) et parfois d'entiers naturels (les éléments de 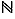 ). Ce n'est qu'exceptionnellement très significatif ; la principale fonction est d'être cohérent avec le reste du monde. Ainsi, comme partout ailleurs, dans ce cours, le nombre
). Ce n'est qu'exceptionnellement très significatif ; la principale fonction est d'être cohérent avec le reste du monde. Ainsi, comme partout ailleurs, dans ce cours, le nombre 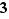 est un nombre premier alors que
est un nombre premier alors que 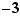 n'en est pas un. En revanche, les nombres négatifs étant autorisés dans la définition de «diviseurs», l'entier
n'en est pas un. En revanche, les nombres négatifs étant autorisés dans la définition de «diviseurs», l'entier 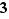 possède en tout et pour tout quatre diviseurs (à savoir
possède en tout et pour tout quatre diviseurs (à savoir 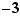 ,
, 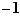 ,
, 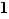 et
et 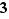 ).
).
Et tout de suite un joli théorème, qui remonte aux Éléments d'Euclide, écrits au IIIème siècle avant notre ère (c'est la proposition 20 du livre IX).
Théorème Il existe une infinité de nombres premiers.
Vous connaissez probablement déjà une démonstration, il en existe plusieurs qui sont toutes bonnes à connaître, en voici une qui est très proche de celle du traité d'Euclide lui-même.
Soit 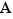 l'ensemble des nombres premiers.
l'ensemble des nombres premiers. 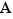 est une partie de
est une partie de 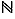 , et est non vide car
, et est non vide car  est premier. On va supposer
est premier. On va supposer 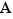 finie et aboutir à une absurdité.
finie et aboutir à une absurdité.
Supposons donc 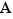 finie. Dès lors que
finie. Dès lors que 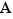 est une partie finie de
est une partie finie de 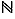 , évidemment non vide car
, évidemment non vide car  est premier,
est premier, 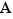 possède un plus grand élément. Notons
possède un plus grand élément. Notons 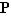 ce plus grand élément, le mystérieux «plus grand nombre premier».
ce plus grand élément, le mystérieux «plus grand nombre premier».
Considérons alors l'entier 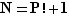 (la factorielle de
(la factorielle de 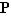 , plus
, plus 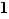 ). Pour tout entier
). Pour tout entier 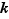 tel que
tel que  , comme
, comme 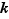 divise
divise 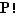 et ne divise pas
et ne divise pas 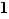 ,
, 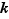 ne peut diviser
ne peut diviser 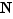 . Tout diviseur de
. Tout diviseur de 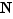 , et en particulier tout diviseur premier de
, et en particulier tout diviseur premier de 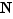 , est donc strictement supérieur à
, est donc strictement supérieur à 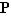 .
.
Or tout entier, et par exemple 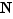 , possède au moins un diviseur premier (pourquoi ? exercice...). Mais alors, chacun de ces diviseurs premiers contredit la maximalité de
, possède au moins un diviseur premier (pourquoi ? exercice...). Mais alors, chacun de ces diviseurs premiers contredit la maximalité de 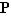 . Absurdité !
. Absurdité !
2. Division euclidienne
Il s'agit de formaliser avec précision la bonne vieille division euclidienne, celle que vous connaissez depuis l'école primaire.
Théorème Soit  un entier (relatif) et
un entier (relatif) et 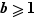 un entier strictement positif. Alors il existe un couple
un entier strictement positif. Alors il existe un couple 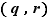 unique (d'entiers) vérifiant la double condition :
unique (d'entiers) vérifiant la double condition :
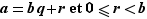
On va prouver successivement l'existence et l'unicité de 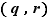 .
.
Existence de 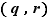 : la démonstration se prête bien à discuter selon le signe de
: la démonstration se prête bien à discuter selon le signe de  . Le cas où
. Le cas où 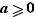 est le cas contenant l'essentiel de la démonstration ; lorsque
est le cas contenant l'essentiel de la démonstration ; lorsque 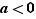 , on ne peut utiliser mot à mot la même preuve, mais on se ramène alors sans mal au cas intéressant déjà traité.
, on ne peut utiliser mot à mot la même preuve, mais on se ramène alors sans mal au cas intéressant déjà traité.
 Premier cas (le cas significatif) : si
Premier cas (le cas significatif) : si 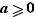 .
.
L'idée de la démonstration est de dire que le quotient de  par
par  est le plus grand entier
est le plus grand entier 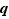 tel que
tel que  soit encore plus petit que
soit encore plus petit que  .
.
Introduisons donc l'ensemble 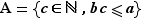 . L'ensemble
. L'ensemble 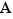 est un ensemble d'entiers naturels ; il est non vide, car il contient
est un ensemble d'entiers naturels ; il est non vide, car il contient  . Il est fini : en effet soit
. Il est fini : en effet soit  un entier tel que
un entier tel que 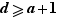 ; on a alors
; on a alors 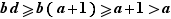 , donc
, donc  et ainsi
et ainsi 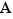 ne contient que des entiers inférieurs ou égaux à
ne contient que des entiers inférieurs ou égaux à  .
.
L'ensemble 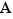 possède donc un plus grand élément
possède donc un plus grand élément 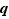 . Posons
. Posons 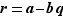 . La première condition sur
. La première condition sur 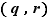 est alors évidemment vérifiée, c'est la seconde qui nécessite une vérification.
est alors évidemment vérifiée, c'est la seconde qui nécessite une vérification.
Comme 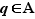 , par définition de
, par définition de 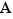 , on a
, on a 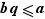 . Donc
. Donc 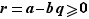 .
.
Comme 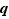 est maximal parmi les éléments de
est maximal parmi les éléments de 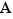 ,
, 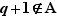 . Donc
. Donc 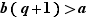 , donc
, donc 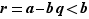 .
.
L'existence est démontrée dans ce cas.
 Second cas (preuve sans imagination) : si
Second cas (preuve sans imagination) : si 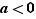 .
.
Posons 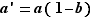 . Comme
. Comme 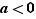 et
et 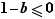 , on obtient
, on obtient 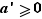 .
.
On peut donc, en appliquant le premier cas, faire la division euclidienne de 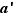 par
par  ; notons
; notons 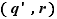 le couple ainsi obtenu : on a alors
le couple ainsi obtenu : on a alors 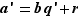 , avec en outre
, avec en outre 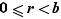 . En réinjectant la définition de
. En réinjectant la définition de 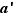 , on écrit alors
, on écrit alors 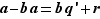 , donc
, donc 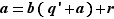 . Si on pose
. Si on pose 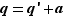 , on constate qu'on a réussi la division euclidienne de
, on constate qu'on a réussi la division euclidienne de  par
par  .
.
Unicité de 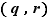 : soit
: soit 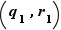 et
et 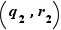 des couples vérifiant les deux conditions exigées dans l'énoncé du théorème.
des couples vérifiant les deux conditions exigées dans l'énoncé du théorème.
On déduit de 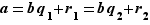 que
que  . Ainsi,
. Ainsi, 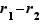 est un multiple de
est un multiple de  .
.
Des conditions 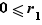 et
et  , on déduit que
, on déduit que 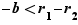 .
.
Des conditions 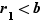 et
et 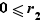 , on déduit que
, on déduit que 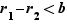 .
.
Ainsi 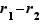 est un multiple de
est un multiple de  compris strictement entre
compris strictement entre  et
et  . La seule possibilité est que
. La seule possibilité est que 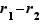 soit nul. On en déduit
soit nul. On en déduit 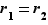 , puis, en allant reprendre l'égalité
, puis, en allant reprendre l'égalité  , que
, que 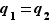 .
.
3. PGCD et PPCM
Les deux théorèmes qui se suivent sont agréablement parallèles ; il est donc amusant de constater que leurs preuves sont plus différentes qu'on ne pourrait s'y attendre. Il est possible de les déduire l'un de l'autre, mais il est instructif de les prouver très séparément. Vous verrez donc plusieurs preuves de l'un comme de l'autre.
Théorème Soit 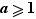 et
et 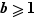 deux entiers. Alors il existe un unique entier
deux entiers. Alors il existe un unique entier 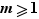 tel que pour tout entier
tel que pour tout entier  ,
,
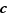 est un multiple de
est un multiple de  et de
et de  si et seulement si
si et seulement si 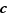 est un multiple de
est un multiple de  .
.
Théorème Soit 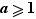 et
et 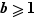 deux entiers. Alors il existe un unique entier
deux entiers. Alors il existe un unique entier 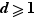 tel que pour tout entier
tel que pour tout entier  ,
,
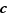 divise
divise  et
et  si et seulement si
si et seulement si 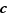 divise
divise  .
.
Ces théorèmes sont vendus avec deux compléments, le premier occasionnellement utile, le second totalement fondamental.
Complément 1 Pour tous  et
et  ,
,  .
.
Complément 2 (Identité de Bézout) Pour tous  et
et  , il existe deux entiers (relatifs)
, il existe deux entiers (relatifs) 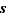 et
et 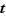 tels que
tels que  .
.
Et tant qu'on y est avant de passer aux démonstrations :
Définition Le plus petit multiple commun de deux entiers  et
et  est l'entier
est l'entier  apparaissant dans l'énoncé du théorème d'existence du PPCM.
apparaissant dans l'énoncé du théorème d'existence du PPCM.
Notation Le plus petit multiple commun de  et
et  sera noté
sera noté  .
.
Définition Le plus grand commun diviseur de deux entiers  et
et  est l'entier
est l'entier  apparaissant dans l'énoncé du théorème d'existence duPGCD.
apparaissant dans l'énoncé du théorème d'existence duPGCD.
Notation Le plus grand commun diviseur de  et
et  sera noté
sera noté 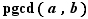 .
.
Première démonstration du théorème d'existence du PPCM
Cette démonstration est la plus élémentaire ; elle consiste à choisir pour  le multiple commun de
le multiple commun de  et
et  le plus «petit» au sens de la relation habituelle
le plus «petit» au sens de la relation habituelle 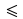 , puis à vérifier qu'il marche. La preuve est en deux parties : d'abord l'existence de
, puis à vérifier qu'il marche. La preuve est en deux parties : d'abord l'existence de  (partie significative) puis son unicité (partie très facile).
(partie significative) puis son unicité (partie très facile).
Existence de 
Introduisons l'ensemble 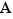 formé des entiers strictement positifs simultanément multiples de
formé des entiers strictement positifs simultanément multiples de  et de
et de  . L'ensemble
. L'ensemble 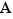 n'est pas vide, puisqu'il contient l'entier
n'est pas vide, puisqu'il contient l'entier  . Il admet donc un plus petit élément
. Il admet donc un plus petit élément  . On va vérifier que cet entier
. On va vérifier que cet entier  convient.
convient.
Pour faire cette vérification, soit un entier 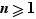 ; nous avons désormais à montrer une équivalence, distinguons méthodiquement les deux sens.
; nous avons désormais à montrer une équivalence, distinguons méthodiquement les deux sens.
 Preuve de l'implication directe : Supposons donc que
Preuve de l'implication directe : Supposons donc que  est un multiple commun de
est un multiple commun de  et
et  , et montrons que
, et montrons que  est un multiple de
est un multiple de  . Pour ce faire, effectuons la division euclidienne de
. Pour ce faire, effectuons la division euclidienne de  par
par  , soit
, soit 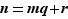 , avec
, avec 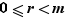 . Comme
. Comme  et
et  sont des multiples de
sont des multiples de  ,
, 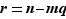 aussi ; de même avec
aussi ; de même avec  . Ainsi
. Ainsi 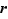 est un multiple commun de
est un multiple commun de  et
et  . Si
. Si 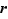 était un entier strictement positif, vu l'inégalité
était un entier strictement positif, vu l'inégalité 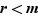 il contredirait la minimalité de
il contredirait la minimalité de  . C'est donc que
. C'est donc que 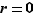 et donc que
et donc que  est un multiple de
est un multiple de  .
.
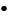 Preuve de l'implication réciproque : Supposons ici que
Preuve de l'implication réciproque : Supposons ici que  est un multiple de
est un multiple de  . Comme
. Comme  est lui-même multiple de
est lui-même multiple de  ,
,  est à son tour multiple de
est à son tour multiple de  ; de même avec
; de même avec  . C'est réglé.
. C'est réglé.
Unicité de 
Soit  et
et 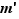 vérifiant les hypothèses du théorème. Comme
vérifiant les hypothèses du théorème. Comme  est un multiple de
est un multiple de  (eh oui !), c'est un multiple commun de
(eh oui !), c'est un multiple commun de  et
et  , donc un multiple de
, donc un multiple de 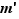 . De même,
. De même, 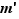 est un multiple de
est un multiple de  . Cela implique que
. Cela implique que  et
et 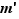 sont forcément égaux au signe près. Comme ils sont tous deux strictement positifs, ils sont égaux. Fin de la démonstration.
sont forcément égaux au signe près. Comme ils sont tous deux strictement positifs, ils sont égaux. Fin de la démonstration.
Voici maintenant une première démonstration de l'existence (et l'unicité) du pgcd, qui l'obtient à partir du ppcm. Cette démonstration a le confort d'être dépourvue d'idée subtile et l'avantage de prouver le Complément 1. Elle a l'inconvénient de ne pas prouver le Complément 2 et de ne pas fournir une méthode rapide de calcul du pgcd.
Première démonstration du théorème d'existence du PGCD
Existence de 
On note  le ppcm de
le ppcm de  et
et  et on pose
et on pose 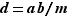 . Remarquons que ce nombre
. Remarquons que ce nombre  est bien un entier : en effet,
est bien un entier : en effet, 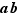 étant un multiple commun évident de
étant un multiple commun évident de  et
et  , c'est un multiple de leur ppcm. Reste à prouver qu'il convient.
, c'est un multiple de leur ppcm. Reste à prouver qu'il convient.
Pour faire cette vérification, soit 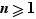 un entier ; nous avons désormais à montrer une équivalence, distinguons méthodiquement les deux sens.
un entier ; nous avons désormais à montrer une équivalence, distinguons méthodiquement les deux sens.
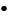 Preuve de l'implication directe : supposons que
Preuve de l'implication directe : supposons que  est un diviseur commun de
est un diviseur commun de  et
et  . On peut donc introduire deux entiers
. On peut donc introduire deux entiers 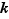 et
et 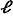 tels que
tels que 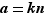 et
et 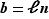 . Pour travailler sur ce sur quoi nous avons des informations, à savoir les multiples de
. Pour travailler sur ce sur quoi nous avons des informations, à savoir les multiples de  et
et  , introduisons le nombre
, introduisons le nombre 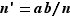 . Ce nombre
. Ce nombre 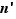 vaut aussi
vaut aussi 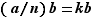 et
et 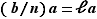 . C'est donc un entier, et même un multiple commun de
. C'est donc un entier, et même un multiple commun de  et
et  . C'est donc un multiple de
. C'est donc un multiple de  . Il existe donc un entier
. Il existe donc un entier 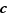 tel que
tel que 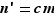 , soit
, soit 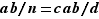 , donc
, donc 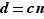 . On a bien prouvé que
. On a bien prouvé que  divise
divise  .
.
 Preuve de l'implication réciproque : puisque
Preuve de l'implication réciproque : puisque 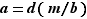 où
où  est un entier,
est un entier,  divise
divise  ; symétriquement puisque
; symétriquement puisque 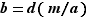 ,
,  divise
divise  . Supposons maintenant que
. Supposons maintenant que  divise
divise  . On voit alors aussitôt que
. On voit alors aussitôt que  divise
divise  et
et  .
.
Unicité de 
C'est exactement le même principe que pour le ppcm, on laisse donc cette partie de la démonstration en exercice (très) facile.
Preuve du Complément 1 : Il tombe immédiatement au vu de la formule qui donne  à partir de
à partir de  . Fin de la démonstration.
. Fin de la démonstration.
Comme promis, voici maintenant une deuxième démonstration du théorème existenceDuPGCD, très différente dans son esprit, et qui permet pour guère plus cher de montrer simultanément le Complément 2.
Deuxième démonstration du théorème d'existence du PGCD
La démonstration est une récurrence sur  ; techniquement, on gagne sérieusement en confort si on autorise
; techniquement, on gagne sérieusement en confort si on autorise  à être nul, ce que l'on n'a pas fait, volontairement, en énonçant le théorème dans l'espoir qu'il soit plus clair. On montrera donc légèrement mieux que l'énoncé de la page précédente, puisqu'on prouvera le résultat sous l'hypothèse «
à être nul, ce que l'on n'a pas fait, volontairement, en énonçant le théorème dans l'espoir qu'il soit plus clair. On montrera donc légèrement mieux que l'énoncé de la page précédente, puisqu'on prouvera le résultat sous l'hypothèse « 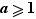 et
et 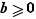 ».
».
Avant de se lancer dans la récurrence proprement dite, on va donner un «résumé de la preuve» sous forme de programme informatique récursif.
Début du programme
* 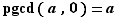 .
.
* Soit 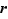 le reste de la division euclidienne de
le reste de la division euclidienne de  par
par  .
.
Les diviseurs communs de  et
et  sont les diviseurs communs de
sont les diviseurs communs de  et
et 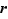 .
.
D'où : * 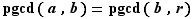 .
.
Fin du programme
Ce résumé de démonstration convaincra peut-être les esprits les plus agiles, mais à notre niveau d'entraînement, il est plus prudent de faire ce qui est derrière les formulations récursives : une bonne vieille récurrence.
On va démontrer par «récurrence forte» sur 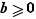 l'hypothèse
l'hypothèse 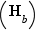 suivante :
suivante : 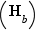 Pour tout entier
Pour tout entier 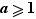 , il existe deux entiers (relatifs)
, il existe deux entiers (relatifs) 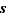 et
et 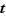 tels que, pour tout
tels que, pour tout 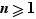 ,
,  divise
divise  et
et  si et seulement si
si et seulement si  divise
divise 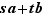 .
.
Vérifions 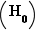 .
.
Soit  un entier avec
un entier avec 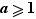 ; tout entier
; tout entier 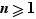 qui divise
qui divise  divise aussi
divise aussi 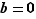 puisque
puisque 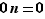 . Pour tout
. Pour tout 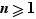 , on a donc :
, on a donc :  divise
divise  et
et  si et seulement si
si et seulement si  divise
divise  . Prenons alors
. Prenons alors 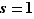 et
et  . On a donc bien pour tout
. On a donc bien pour tout 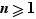 :
:  divise
divise  et
et  si et seulement si
si et seulement si  divise
divise 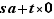 .
.
Soit  un entier fixé, avec
un entier fixé, avec 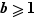 . Supposons la propriété
. Supposons la propriété  vraie pour tout
vraie pour tout 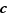 avec
avec  et montrons
et montrons 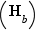 .
.
Soit  un entier avec
un entier avec 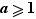 . Notons
. Notons 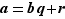 la division euclidienne de
la division euclidienne de  par
par  (qu'on peut réaliser puisque
(qu'on peut réaliser puisque 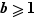 ).
).
Vérifions l'affirmation intermédiaire suivante : pour tout 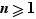 ,
,  est un diviseur commun de
est un diviseur commun de  et
et  si et seulement si
si et seulement si  est un diviseur commun de
est un diviseur commun de  et
et 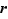 . C'est-à-dire, avec des mots peut-être plus lisibles : «les diviseurs communs de
. C'est-à-dire, avec des mots peut-être plus lisibles : «les diviseurs communs de  et
et  sont les mêmes que ceux de
sont les mêmes que ceux de  et
et 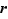 .»
.»
Soit  un diviseur commun de
un diviseur commun de  et
et  , alors
, alors  divise aussi
divise aussi 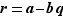 ; réciproquement soit
; réciproquement soit  un diviseur commun de
un diviseur commun de  et
et 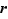 , alors
, alors  divise aussi
divise aussi 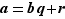 .
.
L'affirmation intermédiaire est donc démontrée.
On peut alors appliquer l'hypothèse de récurrence 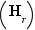 (puisque précisément
(puisque précisément 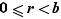 ) sur l'entier
) sur l'entier 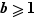 .
.
On en déduit qu'il existe deux entiers relatifs 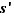 et
et 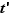 tels que pour tout
tels que pour tout 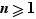 ,
,  divise
divise  et
et 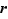 si et seulement si
si et seulement si  divise
divise 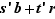 .
.
Remarquons enfin que 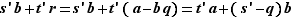 , et qu'ainsi, si on pose
, et qu'ainsi, si on pose  et
et 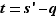 , on a bien prouvé que, pour tout
, on a bien prouvé que, pour tout 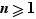 ,
,  divise
divise  et
et  si et seulement si
si et seulement si  divise
divise 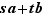 .
.
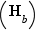 est donc démontrée.
est donc démontrée.
On a donc bien prouvé 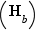 pour tout
pour tout 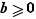 , donc a fortiori pour tout
, donc a fortiori pour tout 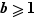 , ce qui prouve le théorème d'existence du PGCD et son Complément 2.
, ce qui prouve le théorème d'existence du PGCD et son Complément 2.
En fait, il reste à prouver l'unicité de  , pour laquelle on renvoie à la démonstration précédente (où on écrivait qu'on la laissait en exercice).
, pour laquelle on renvoie à la démonstration précédente (où on écrivait qu'on la laissait en exercice).
Fin de la démonstration.
À présent, donnons un petit exemple sur des vrais nombres concrets, pour nous soulager l'esprit après tant de lettres.
Calcul du pgcd de 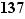 et
et 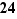
On fait des divisions euclidiennes successives et on écrit dans la colonne de droite les conséquences de ces divisions.
 |
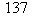 |
 |
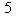 |
 |
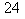 |
 |
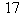 |
 |
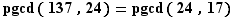 |
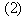 |
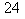 |
 |
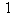 |
 |
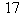 |
 |
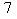 |
 |
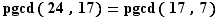 |
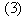 |
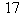 |
 |
 |
 |
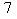 |
 |
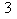 |
 |
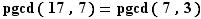 |
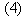 |
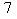 |
 |
 |
 |
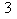 |
 |
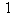 |
 |
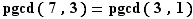 |
Donc  .
.
Ces calculs permettent ensuite sans mal de reconstituer une identité de Bézout.
La dernière division avec un reste non nul est (4) qui donne 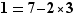 .
.
On va repêcher une expression de 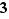 comme un reste dans la relation précédente, soit (3), ce qui donne
comme un reste dans la relation précédente, soit (3), ce qui donne 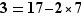 .
.
On reporte cette expression de 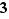 donc
donc 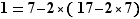 .
.
On regroupe les termes en 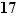 et
et  donc
donc 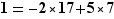 .
.
On va repêcher une expression de  comme un reste dans la relation précédente, soit (2), ce qui donne
comme un reste dans la relation précédente, soit (2), ce qui donne 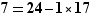 .
.
On reporte cette expression de  donc
donc 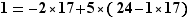 .
.
On regroupe les termes en 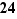 et
et 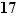 donc
donc  .
.
On va repêcher une expression de 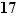 comme un reste dans la relation précédente, soit (1), ce qui donne
comme un reste dans la relation précédente, soit (1), ce qui donne 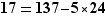 .
.
On reporte cette expression de 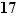 donc
donc 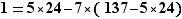 .
.
On regroupe les termes en 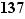 et
et 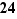 donc
donc 
Et voilà !
Voici un autre exemple.
Calcul du pgcd de  et
et 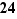
Voici les divisions euclidiennes successives et leurs conséquences en termes de pgcd.
 |
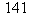 |
 |
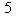 |
 |
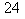 |
 |
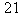 |
 |
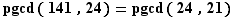 |
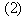 |
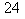 |
 |
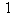 |
 |
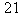 |
 |
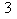 |
 |
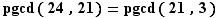 |
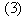 |
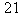 |
 |
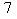 |
 |
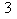 |
 |
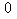 |
 |
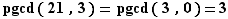 |
Donc 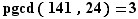 et on vérifiera que ces calculs permettent de reconstituer l'identité de Bézout
et on vérifiera que ces calculs permettent de reconstituer l'identité de Bézout 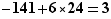
Donnons une dernière définition avant de quitter les pgcd.
Définition On dit que deux entiers 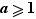 et
et 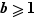 sont premiers entre eux lorsque leur seul diviseur commun positif est
sont premiers entre eux lorsque leur seul diviseur commun positif est 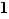 .
.
On veillera à ne pas confondre cette notion avec celle de nombre premier. (Par exemple, les calculs ci-dessus montrent que 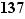 et
et 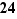 sont premiers entre eux mais
sont premiers entre eux mais 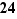 n'est pas premier.)
n'est pas premier.)
4. Lemme de Gauss et décomposition en facteurs premiers
Le lemme de Gauss permet de démontrer l'unicité de la décomposition en facteurs premiers. Ce dernier résultat semble plus facile d'usage pour un utilisateur peu expérimenté, donc on énonce le lemme de Gauss sans commentaire, ou plus exactement sans autre commentaire que ce commentaire négatif.
Lemme Soit  ,
,  et
et 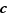 trois entiers strictement positifs. Si
trois entiers strictement positifs. Si  divise le produit
divise le produit 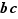 et si
et si  est premier avec
est premier avec 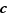 , alors
, alors  divise
divise  .
.
Puisque  est premier avec
est premier avec 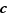 , le pgcd de
, le pgcd de  et
et 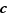 est
est 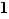 , donc il existe des entiers relatifs
, donc il existe des entiers relatifs 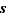 et
et 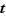 tels que
tels que 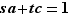 . Multiplions cette identité par
. Multiplions cette identité par  : on obtient
: on obtient 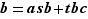 . Mais dans cette écriture,
. Mais dans cette écriture, 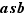 est évidemment multiple de
est évidemment multiple de  tandis que
tandis que  l'est parce que
l'est parce que 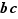 est multiple de
est multiple de  . On en déduit que
. On en déduit que  , somme des deux multiples de
, somme des deux multiples de  que sont
que sont 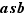 et
et  , est lui-même un multiple de
, est lui-même un multiple de  .
.
Théorème (énoncé approximatif) Tout entier 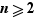 peut être écrit de façon unique comme produit de facteurs premiers.
peut être écrit de façon unique comme produit de facteurs premiers.
L'énoncé est approximatif car il n'est pas si clair de savoir ce que signifie «unique» : on peut écrire 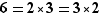 mais il faut évidemment considérer que c'est la même chose. Pour pouvoir comprendre voire utiliser le théorème, cet énoncé suffira bien ; mais pour le démontrer, il faut être plus précis.
mais il faut évidemment considérer que c'est la même chose. Pour pouvoir comprendre voire utiliser le théorème, cet énoncé suffira bien ; mais pour le démontrer, il faut être plus précis.
Théorème (énoncé précis) Tout entier 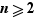 peut être écrit comme produit de facteurs premiers. De plus, si on dispose de deux écritures
peut être écrit comme produit de facteurs premiers. De plus, si on dispose de deux écritures
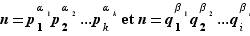
dans lesquelles 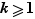 ,
, 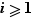 , les entiers
, les entiers 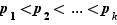 et
et 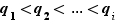 sont tous premiers et rangés en ordre croissant, les exposants
sont tous premiers et rangés en ordre croissant, les exposants 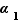 ,
, 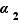 , ...,
, ..., 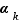 et
et 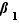 ,
, 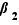 , ...,
, ..., 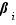 sont tous des entiers strictement positifs, alors ces deux écritures sont les mêmes au sens précis suivant :
sont tous des entiers strictement positifs, alors ces deux écritures sont les mêmes au sens précis suivant : 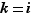 et pour tout
et pour tout 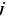 avec
avec 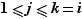 ,
, 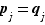 et
et  .
.
À énoncé indigeste, démonstration indigeste.
L'existence provient d'une récurrence élémentaire. Pour tout entier 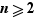 , considérons l'hypothèse de récurrence (forte) suivante :
, considérons l'hypothèse de récurrence (forte) suivante : 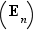 Tout entier
Tout entier  peut s'écrire comme un produit de facteurs premiers comme dans l'énoncé du théorème.
peut s'écrire comme un produit de facteurs premiers comme dans l'énoncé du théorème.
Alors 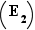 est évidente car
est évidente car  est premier.
est premier.
Soit 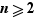 un entier fixé, supposons
un entier fixé, supposons 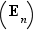 vraie et montrons
vraie et montrons  .
.
Si 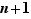 est premier,
est premier,  est évidente.
est évidente.
Si 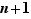 n'est pas premier, il existe un entier
n'est pas premier, il existe un entier  qui divise
qui divise 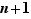 . Notons
. Notons 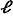 l'entier
l'entier 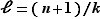 . Alors
. Alors  donc on peut appliquer l'hypothèse
donc on peut appliquer l'hypothèse 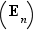 aux deux entiers
aux deux entiers 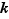 et
et 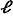 . Il existe donc des entiers premiers
. Il existe donc des entiers premiers 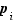 et
et 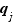 et des exposants
et des exposants 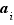 et
et 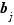 strictement positifs tels que
strictement positifs tels que 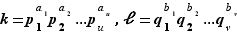 avec
avec  et
et 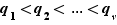 . Par conséquent,
. Par conséquent, 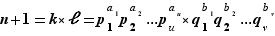 L'ensemble
L'ensemble 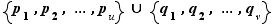 comporte
comporte  éléments. Notons et ordonnons ces éléments comme
éléments. Notons et ordonnons ces éléments comme 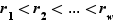 . En regroupant les entiers qui apparaissent dans les deux factorisations, on obtient
. En regroupant les entiers qui apparaissent dans les deux factorisations, on obtient 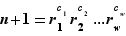 où les exposants
où les exposants 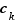 sont définis comme suit :
sont définis comme suit :
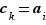 si
si 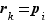 et
et  pour tout
pour tout 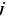 ,
,
 si
si 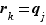 et
et 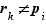 pour tout
pour tout  ,
,
et enfin 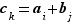 si
si 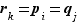 .
.
Donc  est vraie.
est vraie.
Ceci conclut la preuve de l'existence.
Passons à l'unicité. On va donc montrer par récurrence (forte) sur  le résultat d'unicité
le résultat d'unicité 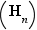 écrit dans l'énoncé du théorème.
écrit dans l'énoncé du théorème.
Démonstration de  , et en fait même de
, et en fait même de 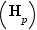 pour tout nombre premier
pour tout nombre premier 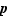
Supposons 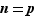 premier écrit sous forme de produit
premier écrit sous forme de produit 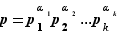 . Chaque
. Chaque 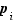 est un diviseur positif de
est un diviseur positif de 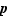 non égal à
non égal à 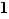 , donc chaque
, donc chaque 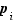 est égal à
est égal à 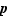 . Ceci entraîne aussitôt que
. Ceci entraîne aussitôt que 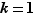 et que
et que 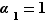 (sans cela le produit serait supérieur ou égal à
(sans cela le produit serait supérieur ou égal à 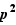 donc distinct de
donc distinct de 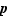 ). L'écriture
). L'écriture 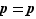 est donc la seule possible pour
est donc la seule possible pour 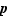 , ce qui démontre
, ce qui démontre 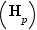 quand
quand 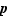 est premier.
est premier.
Soit maintenant  un entier fixé, non premier, avec
un entier fixé, non premier, avec 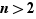 , et supposons l'hypothèse d'unicité
, et supposons l'hypothèse d'unicité 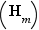 prouvée pour tout entier
prouvée pour tout entier  avec
avec 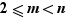 .
.
Première étape Montrons que 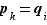 (toujours dans les notations de l'énoncé du théorème).
(toujours dans les notations de l'énoncé du théorème).
Supposons tout d'abord que 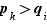 et montrons que l'on aboutit à une absurdité.
et montrons que l'on aboutit à une absurdité.
Puisque les 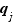 sont supposés rangés dans l'ordre croissant,
sont supposés rangés dans l'ordre croissant,  est alors forcément distinct de tous les
est alors forcément distinct de tous les 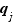 ;
;  et chaque
et chaque 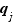 étant premiers, on en conclut que leur seul diviseur commun positif est
étant premiers, on en conclut que leur seul diviseur commun positif est 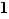 :
:  et
et 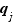 sont donc premiers entre eux.
sont donc premiers entre eux.
Fixons un 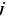 entre
entre 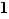 et
et  et montrons par récurrence sur
et montrons par récurrence sur 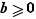 l'énoncé fort intuitif suivant :
l'énoncé fort intuitif suivant : 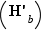 :
:  est premier avec
est premier avec 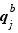 .
.
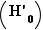 est évident puisque
est évident puisque  .
.
Soit 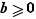 un entier fixé, supposons
un entier fixé, supposons 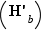 vrai et montrons
vrai et montrons 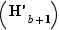 .
.
Si 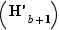 était faux, le pgcd de
était faux, le pgcd de  et
et 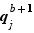 ne serait pas
ne serait pas 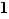 ; comme c'est un diviseur positif de
; comme c'est un diviseur positif de  , ce serait
, ce serait  qui diviserait donc
qui diviserait donc 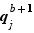 . On peut alors appliquer le lemme de Gauss : comme
. On peut alors appliquer le lemme de Gauss : comme  divise
divise 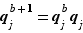 et que
et que  est premier avec
est premier avec 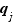 ,
,  divise
divise 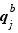 . Mais ceci contredit l'hypothèse
. Mais ceci contredit l'hypothèse 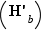 . L'hypothèse
. L'hypothèse 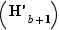 est donc vraie.
est donc vraie.
On a donc bien montré que pour tout 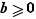 ,
,  est premier avec
est premier avec 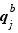 . En particulier,
. En particulier,  est premier avec
est premier avec 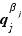 . Comme on a prouvé cette affirmation pour un
. Comme on a prouvé cette affirmation pour un 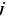 quelconque, on a prouvé que pour tout
quelconque, on a prouvé que pour tout 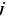 entre
entre 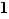 et
et  ,
,  est premier avec
est premier avec 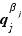 . Ce qu'on a fait avec les puissances de chaque
. Ce qu'on a fait avec les puissances de chaque 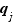 , on va maintenant le recommencer avec le produit de ces puissances. Précisément, on va montrer par récurrence sur l'entier
, on va maintenant le recommencer avec le produit de ces puissances. Précisément, on va montrer par récurrence sur l'entier 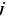 que pour tout
que pour tout 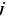 avec
avec 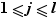 , on a l'énoncé
, on a l'énoncé 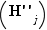 :
:  est premier avec
est premier avec 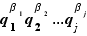 .
.
Les lecteurs encore éveillés (s'il en reste) comprendront que la preuve est à peu près la même que celle des 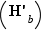 , pour les autres, la voilà :
, pour les autres, la voilà :
Pour  , on doit prouver que
, on doit prouver que  est premier avec
est premier avec 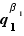 . C'est déjà fait.
. C'est déjà fait.
Fixons un entier 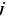 avec
avec 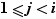 et supposons l'hypothèse
et supposons l'hypothèse 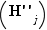 vraie.
vraie.
Si 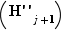 était fausse, le pgcd de
était fausse, le pgcd de  et
et 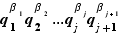 ne serait pas
ne serait pas 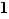 ; comme c'est un diviseur positif de
; comme c'est un diviseur positif de  , ce serait
, ce serait  qui diviserait donc
qui diviserait donc  . On peut alors appliquer le lemme de Gauss : comme
. On peut alors appliquer le lemme de Gauss : comme  divise le nombre
divise le nombre  et comme
et comme  est premier avec
est premier avec 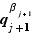 ,
,  divise
divise 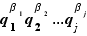 . Mais ceci contredit l'hypothèse
. Mais ceci contredit l'hypothèse 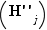 . L'hypothèse
. L'hypothèse 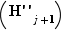 est donc vraie.
est donc vraie.
On a donc montré 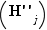 pour tout
pour tout 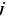 entre
entre 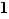 et
et  ; en particulier on a montré
; en particulier on a montré 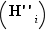 , à savoir que
, à savoir que  est premier avec
est premier avec 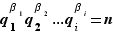 . Mais pourtant
. Mais pourtant  figure dans l'autre décomposition en facteurs premiers de
figure dans l'autre décomposition en facteurs premiers de  (ce n'est pas une illusion d'optique, puisqu'on a pris soin de supposer
(ce n'est pas une illusion d'optique, puisqu'on a pris soin de supposer 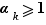 ), donc
), donc  divise
divise  . D'où contradiction. Ouf !
. D'où contradiction. Ouf !
On ne peut donc avoir 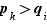 . En échangeant les rôles des coefficients
. En échangeant les rôles des coefficients 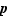 et
et 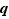 , on voit qu'on ne peut pas non plus avoir
, on voit qu'on ne peut pas non plus avoir 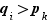 . On en déduit donc que
. On en déduit donc que 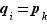 .
.
Fin de la première étape
Deuxième étape On va profiter de ce tout petit morceau d'égalité pour arriver à utiliser l'hypothèse de récurrence et faire tomber toutes les autres égalités requises en cascade.
Notons 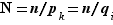 , on a ainsi :
, on a ainsi : 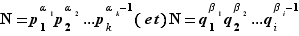 De plus
De plus 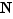 est strictement inférieur à
est strictement inférieur à  , et
, et 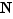 est strictement plus grand que
est strictement plus grand que 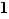 car on a fort opportunément supposé
car on a fort opportunément supposé  non premier. On va donc appliquer l'hypothèse de récurrence
non premier. On va donc appliquer l'hypothèse de récurrence 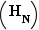 à ces deux écritures de
à ces deux écritures de 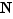 en facteurs premiers. Si on n'est pas méticuleux, on oubliera de s'assurer que tous les exposants sont strictements positifs, et on aura fini tout de suite ; ce sera faux, mais de peu. Hélas, un enseignant scrupuleux ne peut se le permettre et doit donc veiller à ce petit détail, qui nous force à distinguer deux sous-cas.
en facteurs premiers. Si on n'est pas méticuleux, on oubliera de s'assurer que tous les exposants sont strictements positifs, et on aura fini tout de suite ; ce sera faux, mais de peu. Hélas, un enseignant scrupuleux ne peut se le permettre et doit donc veiller à ce petit détail, qui nous force à distinguer deux sous-cas.
Premier sous-cas : 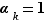 . Dans ce cas, la première écriture de
. Dans ce cas, la première écriture de  se lit en réalité, après effacement du
se lit en réalité, après effacement du 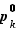 qui l'encombre :
qui l'encombre : 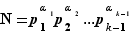 Ainsi
Ainsi 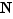 possède une décomposition en facteurs premiers dans laquelle
possède une décomposition en facteurs premiers dans laquelle  ne figure pas. Comme sa décomposition est unique,
ne figure pas. Comme sa décomposition est unique,  ne peut non plus figurer dans l'autre décomposition, et comme
ne peut non plus figurer dans l'autre décomposition, et comme 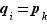 , la seule possibilité est que l'exposant
, la seule possibilité est que l'exposant 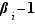 soit nul ; ainsi
soit nul ; ainsi  =1, et les deux représentations
=1, et les deux représentations 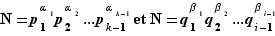 sont deux décompositions de
sont deux décompositions de 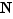 en facteurs premiers. On en déduit que
en facteurs premiers. On en déduit que 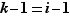 , donc
, donc 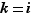 , puis l'égalité de tous les facteurs premiers et exposants encore en attente d'élucidation.
, puis l'égalité de tous les facteurs premiers et exposants encore en attente d'élucidation.
Second sous-cas : 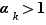 . C'est la même chanson. On remarque tout d'abord qu'on a aussi
. C'est la même chanson. On remarque tout d'abord qu'on a aussi  (sans cela, en échangeant les rôles des coefficients
(sans cela, en échangeant les rôles des coefficients 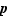 et
et 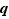 et en utilisant le premier cas, on montrerait que
et en utilisant le premier cas, on montrerait que 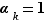 ) ; donc les deux décompositions
) ; donc les deux décompositions 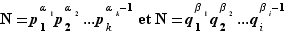 vérifient bien les hypothèses du théorème. Elles sont égales, donc
vérifient bien les hypothèses du théorème. Elles sont égales, donc 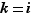 et chaque coefficient
et chaque coefficient 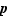 est égal au coefficient
est égal au coefficient 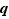 correspondant, avec le même exposant.
correspondant, avec le même exposant.
Fin de la deuxième étape
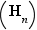 est donc prouvée.
est donc prouvée.
La récurrence est donc terminée, et avec elle la démonstration.
La décomposition en facteurs premiers permet d'énumérer facilement les diviseurs d'un entier.
Proposition Soit  un entier et
un entier et  sa décomposition en facteurs premiers. L'ensemble des diviseurs positifs de
sa décomposition en facteurs premiers. L'ensemble des diviseurs positifs de  est :
est : 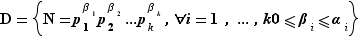
Par exemple l'ensemble des diviseurs positifs de 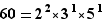 est :
est :
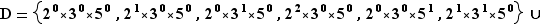
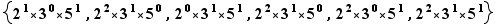
soit, 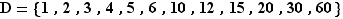 Soit
Soit 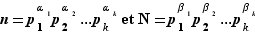 Si pour tout
Si pour tout  ,
, 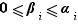 , alors :
, alors : 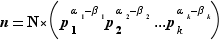 Donc tout élément de l'ensemble
Donc tout élément de l'ensemble 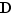 est diviseur de
est diviseur de  .
.
Réciproquement, soit 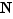 un diviseur de
un diviseur de  . Tout facteur premier de
. Tout facteur premier de 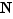 divise
divise  , donc c'est l'un des
, donc c'est l'un des 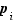 . Si
. Si 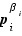 divise
divise 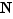 , alors
, alors 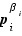 divise aussi
divise aussi  , donc
, donc 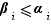 . Ceci montre que tout diviseur de
. Ceci montre que tout diviseur de  est élément de
est élément de 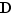 .
.
Quand on connaît la décomposition en facteurs premiers de deux nombres, il est facile de calculer leur pgcd et leur ppcm.
Proposition Soient  et
et  deux entiers. Quitte à admettre des exposants nuls, nous pouvons considérer que leurs facteurs premiers sont les mêmes. Ecrivons donc :
deux entiers. Quitte à admettre des exposants nuls, nous pouvons considérer que leurs facteurs premiers sont les mêmes. Ecrivons donc : 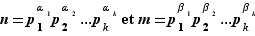 où pour
où pour 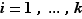 ,
, 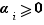 et
et 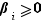 .
.
Alors : 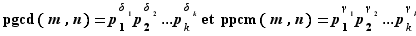 où pour tout
où pour tout 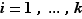 ,
, 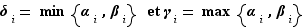
Considérons par exemple : 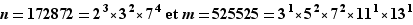 Quitte à admettre des puissances nulles, nous pouvons écrire la décomposition sur les mêmes facteurs.
Quitte à admettre des puissances nulles, nous pouvons écrire la décomposition sur les mêmes facteurs. 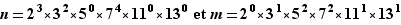 Donc :
Donc : 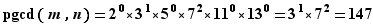 et
et 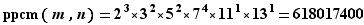
Posons :  On vérifie facilement que
On vérifie facilement que  est bien un diviseur commun de
est bien un diviseur commun de  et de
et de  . Réciproquement, soit
. Réciproquement, soit 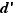 un diviseur commun de
un diviseur commun de  et
et  . Tout facteur premier
. Tout facteur premier 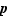 de
de  est aussi un facteur premier de
est aussi un facteur premier de  et de
et de  . Si
. Si  divise
divise  et
et  , alors
, alors 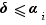 et
et  , donc
, donc 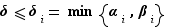 Ceci entraîne que
Ceci entraîne que 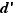 est diviseur de
est diviseur de  . Donc
. Donc  est bien le pgcd de
est bien le pgcd de  et
et  .
.
L'expression du ppcm se déduit de celle du pgcd par la formule : 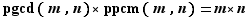
5. Sous-groupes de 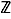
Notation Soit  un entier. On note
un entier. On note 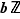 l'ensemble des multiples de
l'ensemble des multiples de  .
.
Par exemple 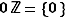 et
et 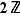 est l'ensemble des entiers relatifs pairs.
est l'ensemble des entiers relatifs pairs.
L'objet de la section est un théorème d'énoncé très simple, et assez pratique.
Théorème Les sous-groupes de 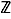 sont exactement les ensembles
sont exactement les ensembles 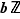 avec
avec 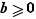 .
.
Il y a deux choses à démontrer : que les ensembles 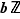 sont des sous-groupes, et que tout sous-groupe est un ensemble
sont des sous-groupes, et que tout sous-groupe est un ensemble 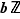 .
.
Commençons donc par vérifier (c'est très facile) que pour 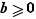 fixé,
fixé, 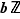 est un sous-groupe de
est un sous-groupe de 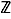 .
.
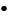
 est multiple de
est multiple de  , donc
, donc 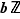 n'est pas vide.
n'est pas vide.
 Soit
Soit 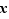 et
et 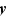 deux éléments de
deux éléments de 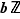 , c'est-à-dire deux multiples de
, c'est-à-dire deux multiples de  . Il est clair que
. Il est clair que 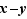 est aussi un multiple de
est aussi un multiple de  , donc appartient à
, donc appartient à 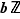 .
.
C'est fait. Pour les amateurs d'abstraction, on pouvait remarquer que 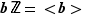 (le sous-groupe engendré par
(le sous-groupe engendré par  ), ce qui est camouflé par la notation additive de l'opération.
), ce qui est camouflé par la notation additive de l'opération.
Soit maintenant 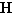 un sous-groupe de
un sous-groupe de 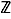 , montrons qu'il existe un entier
, montrons qu'il existe un entier 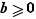 tel que
tel que 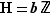 . On distinguera deux cas.
. On distinguera deux cas.
Premier cas : Si 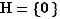 , on remarque que
, on remarque que 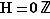 et on a fini.
et on a fini.
Second cas : Si 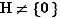 ,
, 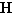 possède au moins un élément non nul
possède au moins un élément non nul 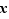 , donc au moins un élément strictement positif
, donc au moins un élément strictement positif 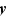 (on prendra
(on prendra 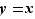 ou
ou  selon le signe de
selon le signe de 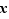 ). Si on introduit l'ensemble
). Si on introduit l'ensemble 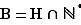 ,
, 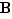 est donc un ensemble d'entiers positifs non vide. Il possède un plus petit élément
est donc un ensemble d'entiers positifs non vide. Il possède un plus petit élément  . On va montrer que
. On va montrer que  convient.
convient.
Il semble raisonnablement clair que 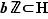 . (Hum, est-ce si clair ou est-ce un petit moment de paresse du rédacteur ? Le lecteur est invité à se forger par lui-même une opinion sur cette épineuse question.)
. (Hum, est-ce si clair ou est-ce un petit moment de paresse du rédacteur ? Le lecteur est invité à se forger par lui-même une opinion sur cette épineuse question.)
Réciproquement soit  un élément de
un élément de 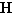 . Si on fait la division euclidienne de
. Si on fait la division euclidienne de  par
par  , soit
, soit 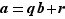 , on en déduit que
, on en déduit que 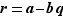 est aussi un élément de
est aussi un élément de 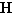 . Comme
. Comme 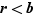 ,
, 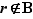 , et comme
, et comme 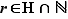 la seule possibilité est que
la seule possibilité est que 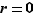 . On en déduit donc que
. On en déduit donc que 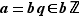 . Ceci prouve l'inclusion
. Ceci prouve l'inclusion 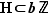 .
.
On a donc montré que 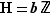 .
.
On a donc montré, dans les deux cas, que 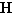 est de la forme
est de la forme 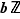 .
.
En application de ce théorème, donnons de nouvelles et élégantes démonstrations des théorèmes existenceDuPPCM et existenceDuPGCD ; l'outil à la base reste la division euclidienne, mais il aura été utilisé une seule fois, dans la preuve du théorème qui précède, et on ne fait plus que d'assez simples manipulations ensemblistes.
Deuxième démonstration du théorème d'existence du PPCM :
Introduisons les sous-groupes de 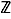 que sont
que sont 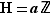 et
et 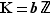 . Pour tout
. Pour tout 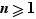 ,
,  est un multiple commun de
est un multiple commun de  et
et  si et seulement si
si et seulement si  est dans
est dans 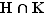 . Or
. Or 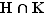 , comme intersection de deux sous-groupes de
, comme intersection de deux sous-groupes de 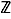 , est lui-même un sous-groupe de
, est lui-même un sous-groupe de 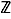 (bon, d'accord, on n'a pas mentionné ce résultat dans le cours sur les sous-groupes, mais on aurait dû, et de toutes façons c'est très facile). Il existe donc un entier
(bon, d'accord, on n'a pas mentionné ce résultat dans le cours sur les sous-groupes, mais on aurait dû, et de toutes façons c'est très facile). Il existe donc un entier 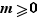 tel que
tel que  (et il est clair que
(et il est clair que 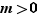 , car
, car 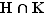 contient d'autres entiers que
contient d'autres entiers que  , par exemple
, par exemple 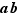 ). On a alors pour tout
). On a alors pour tout 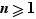 les équivalences :
les équivalences :  est un multiple commun de
est un multiple commun de  et
et  si et seulement si
si et seulement si  appartient à
appartient à 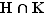 si et seulement si
si et seulement si  appartient à
appartient à 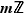 si et seulement si
si et seulement si  est un multiple de
est un multiple de  .
.
L'unicité reste à prouver comme dans la preuve initiale.
Fin de la démonstration.
Troisième démonstration du théorème d'existence du PGCD :
Introduisons l'ensemble 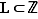 défini par
défini par  .
.
On vérifie sans mal que 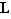 est un sous-groupe de
est un sous-groupe de 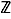 . C'est si facile, qu'on va le laisser au lecteur.
. C'est si facile, qu'on va le laisser au lecteur.
Il existe donc un entier 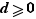 tel que
tel que 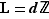 . De plus
. De plus 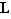 n'est manifestement pas réduit à
n'est manifestement pas réduit à 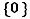 (il contient par exemple
(il contient par exemple 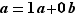 , et même aussi
, et même aussi  ), donc
), donc 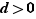 . Montrons que
. Montrons que  convient.
convient.
On a remarqué que  et
et  sont dans
sont dans 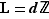 . En d'autres termes, ils sont tous deux multiples de
. En d'autres termes, ils sont tous deux multiples de  , ou, pour dire cela encore autrement,
, ou, pour dire cela encore autrement,  est un diviseur commun de
est un diviseur commun de  et
et  . Il est donc clair que tout diviseur de
. Il est donc clair que tout diviseur de  est à son tour un diviseur commun de
est à son tour un diviseur commun de  et
et  .
.
Par ailleurs,  est dans
est dans 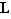 , donc peut être mis sous forme
, donc peut être mis sous forme 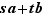 pour des entiers relatifs
pour des entiers relatifs 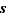 et
et 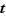 . Si on part d'un diviseur commun
. Si on part d'un diviseur commun 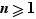 de
de  et
et  ,
, 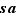 et
et 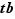 sont à leur tour des multiples de
sont à leur tour des multiples de  , donc aussi
, donc aussi  , et
, et  est donc bien un diviseur de
est donc bien un diviseur de  .
.
Là aussi, on renvoie à la preuve initiale pour l'unicité.
Fin de la démonstration.
6. Congruences
Juste quelques notations pratiques. La section se réduit à quasiment rien.
Définition Soit  et
et  des entiers relatifs et
des entiers relatifs et 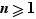 un entier strictement positif. On dit que
un entier strictement positif. On dit que  est congru à
est congru à  modulo
modulo  lorsque
lorsque 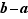 est un multiple de
est un multiple de  .
.
Il est tellement évident de vérifier que, pour  fixé, la relation «est congru à» est une relation d'équivalence sur
fixé, la relation «est congru à» est une relation d'équivalence sur 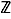 que cet énoncé n'aura pas même l'honneur d'être qualifié de proposition.
que cet énoncé n'aura pas même l'honneur d'être qualifié de proposition.
Notation Lorsque  est congru à
est congru à  modulo
modulo  , on note :
, on note : 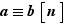
Exemple On repère les jours de l'année par leur numéro de 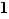 à
à 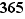 ou
ou 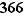 selon les cas. Alors les numéros de tous les lundis sont congrus les uns aux autres modulo
selon les cas. Alors les numéros de tous les lundis sont congrus les uns aux autres modulo  .
.
L'intérêt des congruences est d'être compatibles avec l'addition et la multiplication, au sens suivant :
Proposition Soit 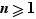 fixé et soit
fixé et soit  ,
,  et
et 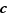 trois entiers relatifs. Alors : si
trois entiers relatifs. Alors : si 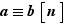 alors
alors 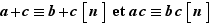
C'est vraiment trop facile.
Exemple 911 Quel est le reste de la division par 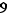 de
de 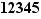 ? On commence par écrire
? On commence par écrire 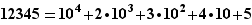 Comme
Comme 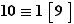 , on en déduit
, on en déduit 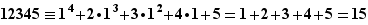 et
et 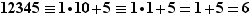 donc la réponse est
donc la réponse est 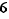 . Et par
. Et par 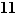 ? Ici, on utilise le fait que
? Ici, on utilise le fait que 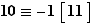 , donc
, donc 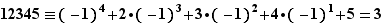 et la réponse est
et la réponse est 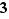 .
.
Exercice : Formaliser les règles de calcul des congruences modulo 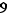 et modulo
et modulo 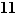 utilisées dans l'exemple 911.
utilisées dans l'exemple 911.
Exercice : Montrer qu'une règle de calcul possible pour calculer des congruences modulo  est la suivante. On décompose l'écriture de
est la suivante. On décompose l'écriture de  en base
en base 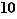 en groupes de
en groupes de 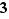 chiffres consécutifs en commençant par le chiffre des unités. Si un bloc vaut
chiffres consécutifs en commençant par le chiffre des unités. Si un bloc vaut 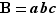 , on note
, on note 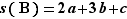 . Puis on effectue la somme alternée
. Puis on effectue la somme alternée  des
des 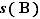 en commençant par le bloc du chiffre des unités. Alors
en commençant par le bloc du chiffre des unités. Alors  et
et  sont congrus modulo
sont congrus modulo  .
.
Par exemple, si 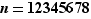 , les blocs sont
, les blocs sont 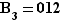 ,
, 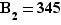 et
et 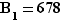 . On calcule
. On calcule 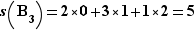 ,
, 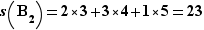 ,
, 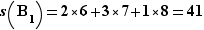 , puis
, puis  donc
donc 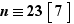 et enfin
et enfin 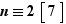 .
.
7. 
En apparence, cette section est consacrée à un formalisme assez gratuit consistant à remplacer l'écriture : 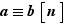 par l'écriture équivalente :
par l'écriture équivalente : 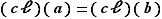 dans
dans  où
où 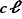 est l'abréviation de «classe». Maigre progrès en apparence ! Toutefois, comme des exemples judicieusement choisis le montreront en fin de section, on a fait plus qu'un simple changement de notations : on a construit un pont entre ce chapitre et le chapitre précédent, pont par lequel on pourra rapatrier des résultats connus sur les groupes pour effectivement affiner notre connaissance des entiers.
est l'abréviation de «classe». Maigre progrès en apparence ! Toutefois, comme des exemples judicieusement choisis le montreront en fin de section, on a fait plus qu'un simple changement de notations : on a construit un pont entre ce chapitre et le chapitre précédent, pont par lequel on pourra rapatrier des résultats connus sur les groupes pour effectivement affiner notre connaissance des entiers.
Définition Soit 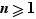 un entier fixé. On appelle
un entier fixé. On appelle  l'ensemble-quotient de
l'ensemble-quotient de 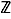 par la relation d'équivalence «est congru à» (modulo
par la relation d'équivalence «est congru à» (modulo  ).
).
Exemple Pour  , soit
, soit  un entier. Si
un entier. Si  est pair, la classe d'équivalence
est pair, la classe d'équivalence 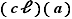 pour la relation de congruence modulo
pour la relation de congruence modulo  est l'ensemble
est l'ensemble 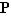 de tous les nombres pairs ; si
de tous les nombres pairs ; si  est impair,
est impair, 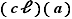 est l'ensemble
est l'ensemble 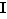 de tous les nombres impairs, et finalement
de tous les nombres impairs, et finalement 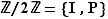
Proposition Pour tout 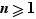 ,
,  possède exactement
possède exactement  éléments.
éléments.
Montrons tout d'abord que 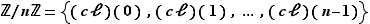 , d'où on déduit aussitôt que
, d'où on déduit aussitôt que  possède au plus
possède au plus  éléments.
éléments.
Soit 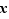 un élément de
un élément de  ; il existe alors
; il existe alors 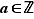 tel que
tel que 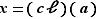 . Effectuons la division euclidienne de
. Effectuons la division euclidienne de  par
par  , soit
, soit  ; on voit alors que
; on voit alors que 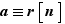 ou encore que
ou encore que 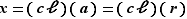 . Mais
. Mais 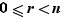 , donc on a bien prouvé que
, donc on a bien prouvé que 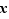 était dans l'ensemble proposé.
était dans l'ensemble proposé.
Montrons maintenant que ces  éléments sont deux à deux distincts, prouvant ainsi que
éléments sont deux à deux distincts, prouvant ainsi que  possède au moins
possède au moins  éléments.
éléments.
Soit  et
et  deux entiers distincts avec
deux entiers distincts avec 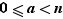 et
et 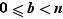 . Des inégalités
. Des inégalités 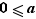 et
et 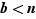 on déduit que
on déduit que 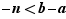 ; des inégalités
; des inégalités 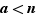 et
et 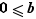 on déduit que
on déduit que 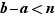 et de l'hypothèse
et de l'hypothèse 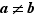 on déduit que
on déduit que 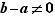 . On en conclut que
. On en conclut que 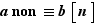 , c'est-à-dire que
, c'est-à-dire que 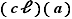 et
et 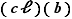 sont deux éléments distincts de
sont deux éléments distincts de  .
.
On a donc bien prouvé que  possède exactement
possède exactement  éléments.
éléments.
Définition Soit 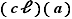 et
et 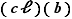 deux éléments de
deux éléments de  . On définit la somme de
. On définit la somme de 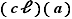 et
et 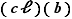 par
par 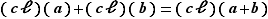 et leur produit par
et leur produit par 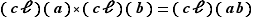 .
.
Prudence ! Cette définition est aussi innocente en apparence que celles qui l'ont précédée. Et pourtant, elle pourrait n'avoir rigoureusement aucun sens.
En effet, la définition de la somme de deux éléments 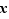 et
et 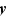 de
de  nécessite implicitement de les mettre préalablement sous forme
nécessite implicitement de les mettre préalablement sous forme 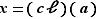 et
et 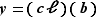 . Mais il y a plusieurs façons de les mettre sous cette forme ! Il faut donc vérifier que la définition ne dépend pas du choix fait dans cette phase préparatoire. Pour montrer à quel point c'est indispensable, donnons une
. Mais il y a plusieurs façons de les mettre sous cette forme ! Il faut donc vérifier que la définition ne dépend pas du choix fait dans cette phase préparatoire. Pour montrer à quel point c'est indispensable, donnons une
Fausse définition (buggée) Soit 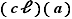 et
et 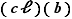 deux éléments de
deux éléments de  . On dira que
. On dira que 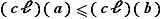 lorsque
lorsque 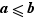 .
.
Il est facile de comprendre pourquoi cette «définition» est bonne pour la corbeille à papier : dans 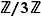 , prenons
, prenons 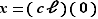 et
et 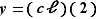 . En les écrivant ainsi, la «définition» nous donne :
. En les écrivant ainsi, la «définition» nous donne :  . Mais on peut aussi écrire
. Mais on peut aussi écrire 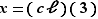 et comme précédemment
et comme précédemment 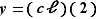 . En s'y prenant ainsi,
. En s'y prenant ainsi, 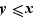 . Cette «définition» n'a donc en fait aucun sens.
. Cette «définition» n'a donc en fait aucun sens.
Sermon (ou : Prudence II, le retour) Malgré ses dehors anecdotiques, il est indispensable de comprendre cette remarque. La fausse définition et la bonne sont semblables formellement, alors que l'une est absurde et l'autre non. Fin du sermon.
Procédons donc à cette indispensable vérification. Soit 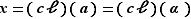 et
et 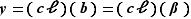 deux éléments de
deux éléments de  . La cohérence de la définition exige de prouver que
. La cohérence de la définition exige de prouver que 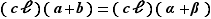 . La vérification est alors évidente
. La vérification est alors évidente 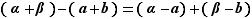 étant un multiple de
étant un multiple de  parce que
parce que 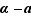 et
et 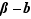 le sont tous les deux. De même
le sont tous les deux. De même 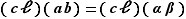 car
car 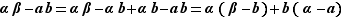 .
.
Ainsi au point où nous en sommes,  est muni d'une addition et d'une multiplication. Traçons un exemple de tables, pour voir quelle tête elles ont. Ce sera l'exemple de
est muni d'une addition et d'une multiplication. Traçons un exemple de tables, pour voir quelle tête elles ont. Ce sera l'exemple de 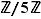 .
.
On note dans cette table et dans les suivantes 
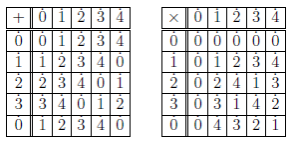
Après la présentation de l'objet, un peu de théorie à son sujet.
Proposition Pour tout 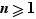 ,
,  est un anneau commutatif.
est un anneau commutatif.
Elle est d'un ennui mortel, et ne présente aucune difficulté. Pour en faire un tout petit bout, montrons que l'addition est associative : soit 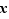 ,
, 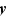 et
et 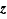 trois éléments de
trois éléments de  . On peut les écrire sous forme
. On peut les écrire sous forme 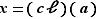 ,
, 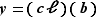 ,
, 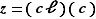 . Vu la définition de l'addition dans
. Vu la définition de l'addition dans  , on a alors
, on a alors
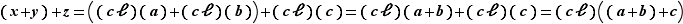
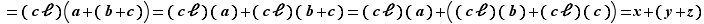
Et toutes les vérifications seraient de ce genre. Nous décidons donc de les laisser au lecteur.
Plus intéressant et légèrement plus subtil est le résultat suivant.
Théorème Pour tout 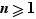 ,
,  est un corps commutatif si et seulement si
est un corps commutatif si et seulement si  est un nombre premier.
est un nombre premier.
Montrons tour à tour les deux sens de l'équivalence.
Preuve de l'implication directe. On va montrer cette implication par contraposition. Supposons donc que  n'est pas premier, et montrons que
n'est pas premier, et montrons que  n'est pas un corps commutatif (on verra même en passant que ce n'est même pas un anneau intègre).
n'est pas un corps commutatif (on verra même en passant que ce n'est même pas un anneau intègre).
Traitons à part le cas, «stupide», où  vaudrait
vaudrait 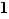 . Dans ce cas,
. Dans ce cas, 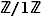 ne possède qu'un élément, donc n'est pas un corps commutatif.
ne possède qu'un élément, donc n'est pas un corps commutatif.
Examinons le cas, significatif, où  n'est pas premier, mais n'est pas non plus égal à
n'est pas premier, mais n'est pas non plus égal à 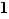 . Dans ce cas, on peut écrire
. Dans ce cas, on peut écrire 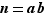 , où
, où  et
et 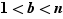 . Dans l'anneau
. Dans l'anneau  , on obtient alors la relation
, on obtient alors la relation 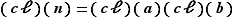 , soit
, soit 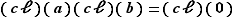 . Pourtant, au vu des inégalités vérifiées par
. Pourtant, au vu des inégalités vérifiées par  et
et  , ni
, ni 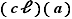 ni
ni 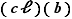 n'est nul. Donc
n'est nul. Donc  n'est pas intègre, et a fortiori n'est pas un corps commutatif.
n'est pas intègre, et a fortiori n'est pas un corps commutatif.
On a bien prouvé dans les deux cas que  n'est pas un corps commutatif.
n'est pas un corps commutatif.
Preuve de l'implication inverse. Supposons  premier, et montrons que
premier, et montrons que  est alors un corps commutatif.
est alors un corps commutatif.
Nous savons déjà que la multiplication sur  est commutative.
est commutative.
Comme  possède
possède  éléments, il en possède au moins deux.
éléments, il en possède au moins deux.
Soit 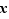 un élément non nul de
un élément non nul de  . On peut écrire
. On peut écrire 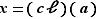 pour un entier
pour un entier  dans l'ensemble
dans l'ensemble 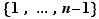 . Puisque
. Puisque  est premier,
est premier,  ne possède d'autre diviseur positif commun avec
ne possède d'autre diviseur positif commun avec  que
que 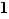 et donc
et donc  et
et  sont premiers entre eux. Il existe donc deux entiers relatifs
sont premiers entre eux. Il existe donc deux entiers relatifs 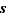 et
et 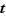 tels que
tels que 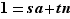 . En passant aux classes d'équivalence, on obtient :
. En passant aux classes d'équivalence, on obtient : 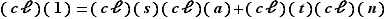 , soit
, soit 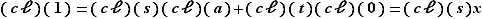 .
.
On a donc trouvé un inverse de 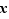 , à savoir
, à savoir 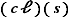 .
.
Finalement,  est donc bien un corps commutatif.
est donc bien un corps commutatif.
Remarque On retiendra de cette démonstration la technique pratique de calcul de l'inverse d'un élément non nul de  : écrire une identité de Bézout entre un représentant de cet élément et
: écrire une identité de Bézout entre un représentant de cet élément et  , et redescendre aux classes d'équivalence.
, et redescendre aux classes d'équivalence.
Et voilà, on sait tout. Reste à donner quelques illustrations afin de convaincre de l'utilité de l'introduction de cette notion abstraite.
Exemple Résoudre dans 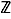 l'équation suivante, d'inconnue
l'équation suivante, d'inconnue 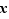 :
: 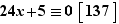 On peut traiter cet exemple avec ou sans usage de
On peut traiter cet exemple avec ou sans usage de  . Faisons les deux successivement ; on constatera que les énoncés simples sur les propriétés algébriques de
. Faisons les deux successivement ; on constatera que les énoncés simples sur les propriétés algébriques de  remplacent avantageusement les techniques, il est vrai elles aussi simples, d'arithmétique classique.
remplacent avantageusement les techniques, il est vrai elles aussi simples, d'arithmétique classique.
Première résolution (sans  )
)
Remarquons que 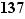 est premier, et donc que
est premier, et donc que 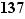 et
et 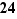 sont premiers entre eux ; cherchons à écrire une identité de Bézout entre 137 et 24 ; en utilisant l'algorithme décrit plus haut, on découvre que :
sont premiers entre eux ; cherchons à écrire une identité de Bézout entre 137 et 24 ; en utilisant l'algorithme décrit plus haut, on découvre que :  d'où on déduit (par une simple multiplication par
d'où on déduit (par une simple multiplication par 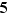 ) que :
) que :  Reportons cette identité dans l'équation, qui devient donc :
Reportons cette identité dans l'équation, qui devient donc : 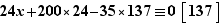 À son tour, cette équation est équivalente à la condition suivante :
À son tour, cette équation est équivalente à la condition suivante : 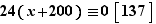 qui signifie que 137 divise
qui signifie que 137 divise 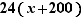 , donc, en utilisant le lemme de Gauss puisque 137 et 24 sont premiers entre eux, que 137 divise
, donc, en utilisant le lemme de Gauss puisque 137 et 24 sont premiers entre eux, que 137 divise 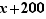 . Finalement,
. Finalement, 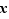 est solution si et seulement si
est solution si et seulement si 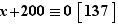 , c'est-à-dire
, c'est-à-dire 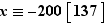 , c'est-à-dire
, c'est-à-dire  .
.
Deuxième résolution (avec  )
)
Remarquons que 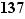 est premier, et donc que
est premier, et donc que  est un corps commutatif. Faisons tous les calculs dans ce corps.
est un corps commutatif. Faisons tous les calculs dans ce corps.
L'équation proposée se réécrit 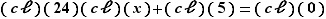 , soit
, soit 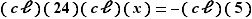 , soit
, soit 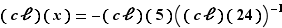 .
.
Calculons donc 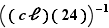 ; pour cela nous connaissons la bonne méthode : écrire une identité de Bézout entre
; pour cela nous connaissons la bonne méthode : écrire une identité de Bézout entre 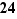 et
et 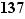 , à savoir
, à savoir  puis redescendre aux classes d'équivalence dans
puis redescendre aux classes d'équivalence dans  :
: 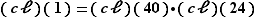 soit :
soit : 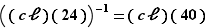
On en conclut que l'équation proposée équivaut à : 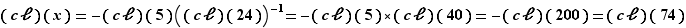
Exemple Résoudre dans  l'équation suivante, d'inconnue
l'équation suivante, d'inconnue 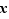 :
: 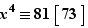 Là aussi, écrire deux solutions serait possible, mais celle utilisant
Là aussi, écrire deux solutions serait possible, mais celle utilisant  est tellement plus agréable à écrire que l'on s'en contentera.
est tellement plus agréable à écrire que l'on s'en contentera.
Tout d'abord, l'équation s'écrit 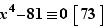 et, dans
et, dans 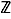 ,
, 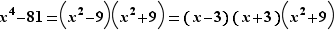 Dans
Dans  , l'équation s'écrit donc
, l'équation s'écrit donc 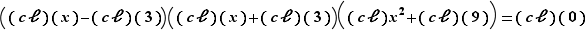 Mais
Mais 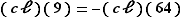 donc
donc 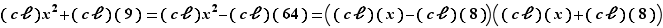 Finalement, en utilisant
Finalement, en utilisant 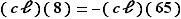 et
et 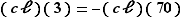 , on voit que l'équation de départ s'écrit
, on voit que l'équation de départ s'écrit
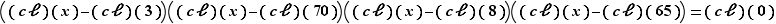
soit 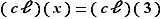 ou
ou  ou
ou 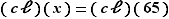 ou
ou 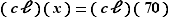 , car
, car  est un corps commutatif, donc intègre.
est un corps commutatif, donc intègre.
Les solutions de l'équation proposée sont donc 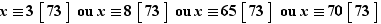
Exemple Résoudre dans  l'équation suivante, d'inconnue
l'équation suivante, d'inconnue 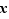 :
: 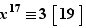 Là encore, on ne saurait trop recommander le passage dans
Là encore, on ne saurait trop recommander le passage dans 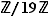 . L'équation s'écrit dès lors :
. L'équation s'écrit dès lors : 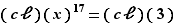 . Notons
. Notons  l'inconnue auxiliaire
l'inconnue auxiliaire 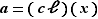 et remarquons que
et remarquons que  . Il suffit donc de résoudre
. Il suffit donc de résoudre  dans
dans 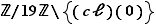 .
.
Mais, si  , alors
, alors  si et seulement si
si et seulement si 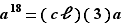 . Maintenant, pour tout
. Maintenant, pour tout  dans le groupe multiplicatif
dans le groupe multiplicatif 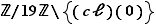 , on sait que l'ordre de
, on sait que l'ordre de  , qui est le nombre d'éléments du groupe
, qui est le nombre d'éléments du groupe  , divise le nombre d'éléments de
, divise le nombre d'éléments de 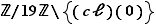 , c'est-à-dire
, c'est-à-dire 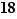 .
.
Ainsi, pour tout élément  de
de 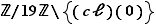 ,
, 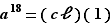 . L'équation étudiée se simplifie donc grandement en
. L'équation étudiée se simplifie donc grandement en  , c'est-à-dire
, c'est-à-dire 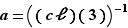 . Sa résolution se ramène donc à la recherche de l'inverse de
. Sa résolution se ramène donc à la recherche de l'inverse de 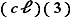 dans
dans 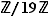 ; on écrit alors une relation de Bézout :
; on écrit alors une relation de Bézout : 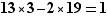 et on en déduit que
et on en déduit que 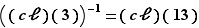 .
.
Finalement les solutions de l'équation initiale sont donc 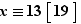
Exemple Résoudre dans 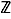 l'équation suivante, d'inconnue
l'équation suivante, d'inconnue 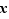 :
: 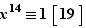 Ce sont les mêmes idées que dans l'exemple précédent qui font marcher cet exercice, en un peu plus astucieux encore.
Ce sont les mêmes idées que dans l'exemple précédent qui font marcher cet exercice, en un peu plus astucieux encore.
Comme dans l'exemple prédédent, on commence par passer dans 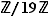 , où l'équation s'écrit dès lors :
, où l'équation s'écrit dès lors : 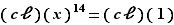 . On note
. On note 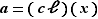 , on remarque que
, on remarque que 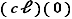 n'est pas solution, et on décide donc de résoudre
n'est pas solution, et on décide donc de résoudre 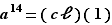 dans
dans 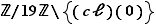 .
.
Maintenant, on remarque que pour tout  de
de 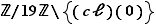 , dire que
, dire que 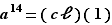 équivaut à dire que l'ordre de
équivaut à dire que l'ordre de  divise
divise 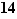 . Par ailleurs, comme dans l'exemple précédent, pour tout élément
. Par ailleurs, comme dans l'exemple précédent, pour tout élément  de
de 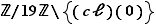 , l'ordre de
, l'ordre de  divise
divise 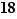 . Ainsi, l'ordre de
. Ainsi, l'ordre de  divise
divise 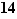 si et seulement s'il divise
si et seulement s'il divise 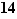 et
et 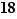 , donc si et seulement s'il divise
, donc si et seulement s'il divise  .
.
On a donc montré que pour tout  de
de 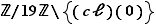 ,
, 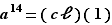 si et seulement si
si et seulement si 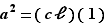 .
.
Cette nouvelle équation est alors très facile à résoudre : 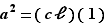 si et seulement si
si et seulement si 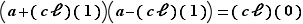 si et seulement si
si et seulement si 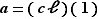 ou
ou 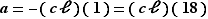 .
.
Les solutions de l'équation initiale sont donc