Site http://www.epsilon-publi.net/
- espace http://www.epsilon-publi.net/w/webmaster/ de
|
Pour visualiser le document avec epsilonwriter, cliquer ici |
Copier-coller et glisser-déposer
Tutoriel de découverte d'epsilonwriter
Copier-coller à une position de curseur
1) Coller 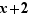 à droite de
à droite de 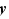 dans :
dans :
 |
Pour cela, sélectionner 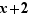 , copier avec Ctrl+C ou le menu "Edition | Copier" puis placer le curseur à droite de
, copier avec Ctrl+C ou le menu "Edition | Copier" puis placer le curseur à droite de 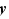 et coller avec Ctrl+V ou le menu "Edition | Coller".
et coller avec Ctrl+V ou le menu "Edition | Coller".
On obtient  propositions : collage derrière
propositions : collage derrière 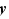 avec
avec 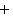

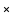 ainsi que collage par fraction avec
ainsi que collage par fraction avec 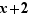 au dénominateur.
au dénominateur.
2) Coller 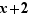 à gauche de
à gauche de 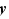 dans :
dans :
 |
On obtient  propositions : collage devant
propositions : collage devant 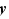 avec
avec 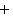

 ainsi que collage par fraction avec
ainsi que collage par fraction avec 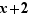 au numérateur.
au numérateur.
3) Coller  à droite de
à droite de  dans :
dans :
 |
On obtient  propositions : collage avec "et" "ou"
propositions : collage avec "et" "ou"  ainsi que collage par système d'équation avec
ainsi que collage par système d'équation avec  en-dessous.
en-dessous.
4) Coller 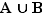 à droite de
à droite de 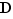 dans :
dans :
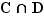 |
On obtient 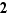 propositions : collage avec
propositions : collage avec 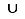 ainsi que
ainsi que 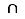
Copier-coller sur "?" ou sur une sélection
5) Coller 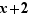 sur "?" dans :
sur "?" dans :
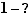 |
On obtient  : le collage sur "?" effectue une substitution mathématique.
: le collage sur "?" effectue une substitution mathématique.
6) Coller 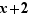 sur
sur 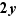 dans :
dans :
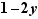 |
Pour cela, sélectionner 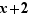 , copier puis sélectionner
, copier puis sélectionner 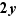 et coller.
et coller.
On obtient  : le collage sur une sélection effectue une substitution mathématique.
: le collage sur une sélection effectue une substitution mathématique.
Glisser-déposer
7) Effectuer un glisser-déposer de 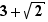 à droite de
à droite de 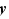 dans :
dans :
 |
Pour cela, sélectionner 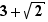 dans le rectangle, attraper la sélection en enfonçant le bouton gauche de la souris, déplacer le curseur à droite de
dans le rectangle, attraper la sélection en enfonçant le bouton gauche de la souris, déplacer le curseur à droite de 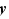 et relâcher le bouton.
et relâcher le bouton.
On obtient un popup avec  propositions identiques à celles d'un collage.
propositions identiques à celles d'un collage.
8) Effectuer le même glisser-déposer mais en appuyant sur la touche Ctrl pendant le collage :
 |
La dépose est identique, mais 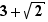 n'a pas été enlevé de sa position initiale.
n'a pas été enlevé de sa position initiale.