Site http://www.epsilon-publi.net/
- espace http://www.epsilon-publi.net/b/bycart/ de B. Ycart, professeur de mathématique, Université Joseph-Fourier
|
Pour visualiser le document avec epsilonwriter, cliquer ici |
Les nombres réels
Bernard Ycart
Licence CC-BY
Origine : M@ths en ligne - Université Joseph Fourier
Document produit en ouvrant un fichier Tex
Mots-clés: réel, addition, multiplication, ordre, borne, majorant, minorant, rationnel, irrationnel, approximation
Sommaire
Vous savez déjà compter, et vous connaissez les propriétés des réels. Une seule nouveauté dans ce chapitre, la notion de borne (supérieure ou inférieure) d'un ensemble. Au-delà des définitions, vous allez commencer à vous habituer aux «epsilons strictement positifs», à comprendre comme des quantités pouvant prendre des valeurs arbitrairement petites. À part ça, pas grand chose de neuf ni de difficile dans ce chapitre d'introduction à l'analyse.
1. Opérations
Nous ne présenterons pas de construction axiomatique de l'ensemble 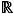 des nombres réels. Cette section rappelle quelques notations, les propriétés des opérations (addition, multiplication) et de la relation d'ordre.
des nombres réels. Cette section rappelle quelques notations, les propriétés des opérations (addition, multiplication) et de la relation d'ordre.
Nous utilisons les notations classiques suivantes pour les ensembles emboîtés de nombres  .
.
 |
 |
 |
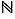 |
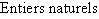 |
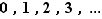 |
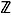 |
 |
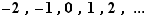 |
 |
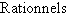 |
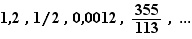 |
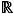 |
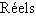 |
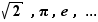 |
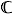 |
 |
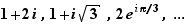 |
L'exposant  signifie «privé de
signifie «privé de 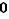 ». Ainsi,
». Ainsi, 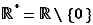 ,
, 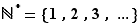 .
.
Pour les calculs usuels (à la main, sur les calculettes ou par ordinateur), ce sont forcément des nombres décimaux, donc rationnels, que l'on manipule. Pourtant l'ensemble  n'est pas un cadre de calcul mathématiquement suffisant, pour plusieurs raisons, qui seront énoncées dans la suite de ce chapitre. La première, reconnue dès l'antiquité grecque, est que certaines quantités, qui pourtant apparaissent couramment en géométrie élémentaire, ne s'expriment pas comme rapports d'entiers. La plus simple est la diagonale d'un carré de côté
n'est pas un cadre de calcul mathématiquement suffisant, pour plusieurs raisons, qui seront énoncées dans la suite de ce chapitre. La première, reconnue dès l'antiquité grecque, est que certaines quantités, qui pourtant apparaissent couramment en géométrie élémentaire, ne s'expriment pas comme rapports d'entiers. La plus simple est la diagonale d'un carré de côté 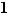 , à savoir
, à savoir 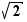 : nous verrons plus loin que
: nous verrons plus loin que 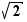 n'est pas un nombre rationnel;
n'est pas un nombre rationnel; 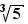 ,
, 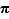 , ou
, ou 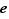 n'en sont pas non plus.
n'en sont pas non plus.
Les propriétés de l'addition, de la multiplication et de la relation d'ordre sont rappelées ci-dessous.
Addition
 Associativité :
Associativité : 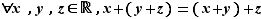
 Élément neutre :
Élément neutre : 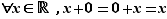
 Opposé :
Opposé : 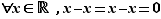
 Commutativité :
Commutativité : 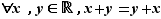
L'ensemble des réels muni de l'addition est un groupe commutatif.
Multiplication
L'ensemble 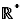 (ensemble des réels privé de
(ensemble des réels privé de 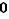 ), muni de la multiplication, est un autre groupe commutatif.
), muni de la multiplication, est un autre groupe commutatif.
 Associativité :
Associativité : 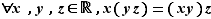
 Élément neutre :
Élément neutre : 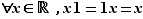
 Inverse :
Inverse : 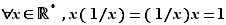
 Commutativité :
Commutativité : 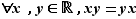
 Distributivité :
Distributivité : 
L'ensemble des réels muni de l'addition et de la multiplication est un corps commutatif.
Relation d'ordre
 Réflexivité :
Réflexivité : 
 Transitivité :
Transitivité : 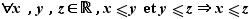
 Antisymétrie :
Antisymétrie : 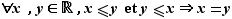
 Ordre total :
Ordre total : 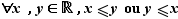
Les trois premières propriétés définissent une relation d'ordre. Ici l'ordre est total car deux réels quelconques peuvent toujours être comparés.
Pour des raisons de commodité, on utilise aussi couramment les notations 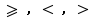 :
:
 |
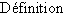 |
 |
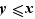 |
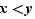 |
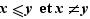 |
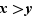 |
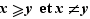 |
On utilise aussi les ensembles de réels notés 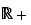 ,
, 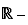 ,
,  et
et  .
.
 |
 |
 |
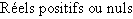 |
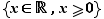 |
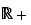 |
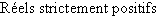 |
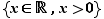 |
 |
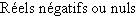 |
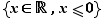 |
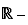 |
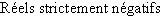 |
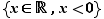 |
 |
La relation d'ordre est compatible avec l'addition par un réel quelconque, et avec la multiplication entre réels positifs.

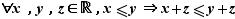

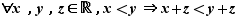

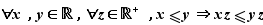

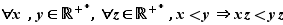
Comme conséquence de ces relations de compatibilité, on obtient les règles suivantes qui permettent de combiner des inégalités. 
On peut donc ajouter deux inégalités de même sens (attention : on ne peut pas ajouter deux inégalités de sens opposés ni soustraire deux inégalités de même sens).
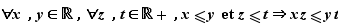
On peut multiplier deux inégalités de même sens, si elles concernent des réels positifs ou nuls. (attention : on ne peut pas mutiplier deux inégalités de sens opposés, ni diviser des inégalités de même sens, ni multiplier des inégalités qui concernent des réels négatifs). Pour se ramener à des inégalités de même sens, ou à des réels positifs, il peut être utile de changer de signe ou de passer à l'inverse.

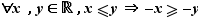

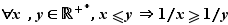
2. Bornes
Définition Soit  une partie de
une partie de 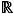 et
et 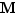 un réel. On dit que
un réel. On dit que 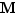 est un majorant de
est un majorant de  si :
si : 
De même, 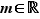 est un minorant de
est un minorant de  si :
si : 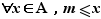
On dit qu'un ensemble de réels  admet un plus grand élément (respectivement plus petit élément) s'il existe
admet un plus grand élément (respectivement plus petit élément) s'il existe  tel que pour tout
tel que pour tout 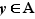 ,
, 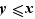 (respectivement :
(respectivement : 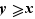 ). Donc le plus grand élément (s'il existe il est nécessairement unique) est à la fois un majorant de
). Donc le plus grand élément (s'il existe il est nécessairement unique) est à la fois un majorant de  et un élément de
et un élément de  . Le fait que l'ordre sur
. Le fait que l'ordre sur 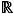 soit total entraîne que tout ensemble fini de réels admet un plus petit élément et un plus grand élément. Si
soit total entraîne que tout ensemble fini de réels admet un plus petit élément et un plus grand élément. Si 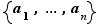 est un ensemble fini de réels, nous noterons
est un ensemble fini de réels, nous noterons  le plus petit et
le plus petit et 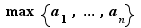 le plus grand élément. Nous réserverons les notations
le plus grand élément. Nous réserverons les notations 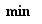 et
et 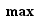 aux ensembles finis. Un ensemble infini de réels n'admet pas nécessairement de plus petit ou de plus grand élément. Voici quelques exemples.
aux ensembles finis. Un ensemble infini de réels n'admet pas nécessairement de plus petit ou de plus grand élément. Voici quelques exemples.
 |
 |
 |
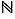 |
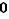 |
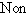 |
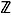 |
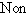 |
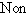 |
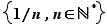 |
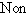 |
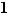 |
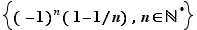 |
 |
 |
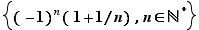 |
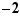 |
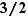 |
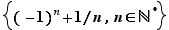 |
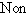 |
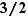 |
 |
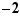 |
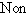 |
Non seulement 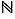 n'a pas de plus grand élément mais de plus aucun réel n'est plus grand que tous les éléments de
n'a pas de plus grand élément mais de plus aucun réel n'est plus grand que tous les éléments de 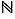 . Par contre, les 5 derniers ensembles du tableau ci-dessus sont bornés au sens suivant.
. Par contre, les 5 derniers ensembles du tableau ci-dessus sont bornés au sens suivant.
Définition Soit  une partie de
une partie de 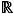 (un ensemble de réels). On dit que
(un ensemble de réels). On dit que  est :
est :
 majorée s'il existe un majorant de
majorée s'il existe un majorant de  ,
,
 minorée s'il existe un minorant de
minorée s'il existe un minorant de  ,
,
 bornée si
bornée si  est à la fois majorée et minorée.
est à la fois majorée et minorée.
Si 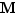 est un majorant de
est un majorant de  , alors
, alors 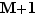 ,
, 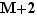 et plus généralement tout réel plus grand que
et plus généralement tout réel plus grand que 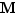 sont aussi des majorants. Nous admettrons pour l'instant le théorème suivant, dont nous donnerons une démonstration dans la section 1.6.
sont aussi des majorants. Nous admettrons pour l'instant le théorème suivant, dont nous donnerons une démonstration dans la section 1.6.
Théorème Soit  une partie non vide de
une partie non vide de 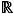 .
.
Si  est majorée, alors l'ensemble des majorants de
est majorée, alors l'ensemble des majorants de  admet un plus petit élément.
admet un plus petit élément.
Si  est minorée, alors l'ensemble des minorants de
est minorée, alors l'ensemble des minorants de  admet un plus grand élément.
admet un plus grand élément.
Définition Soit  une partie non vide de
une partie non vide de 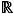 .
.
Si  est majorée, on appelle borne supérieure de
est majorée, on appelle borne supérieure de  et on note
et on note 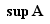 le plus petit des majorants de
le plus petit des majorants de  .
.
Si  est minorée, on appelle borne inférieure de
est minorée, on appelle borne inférieure de  et on note
et on note 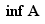 le plus grand des minorants de
le plus grand des minorants de  .
.
Du fait que l'ordre des réels est total, la borne supérieure et la borne inférieure, si elles existent, sont nécessairement uniques. Lorsque  admet un plus grand élément, la borne supérieure de
admet un plus grand élément, la borne supérieure de  est ce plus grand élément. Lorsque
est ce plus grand élément. Lorsque  admet un plus petit élément, la borne inférieure de
admet un plus petit élément, la borne inférieure de  est ce plus petit élément. On étend la définition de
est ce plus petit élément. On étend la définition de 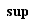 et
et 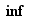 aux ensembles non majorés et non minorés par la convention suivante.
aux ensembles non majorés et non minorés par la convention suivante.
Si  n'est pas majorée,
n'est pas majorée, 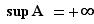
Si  n'est pas minorée,
n'est pas minorée, 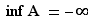
Reprenons comme exemples les 6 ensembles du tableau précédent.
 |
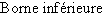 |
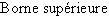 |
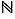 |
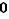 |
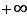 |
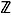 |
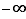 |
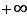 |
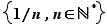 |
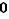 |
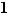 |
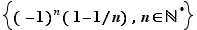 |
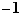 |
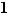 |
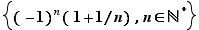 |
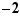 |
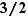 |
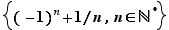 |
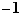 |
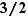 |
 |
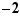 |
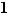 |
Dans le cas où  est majorée et n'admet pas de plus grand élément, alors
est majorée et n'admet pas de plus grand élément, alors 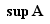 n'appartient pas à
n'appartient pas à  , mais on trouve néanmoins des éléments de
, mais on trouve néanmoins des éléments de  arbitrairement proches de la borne supérieure.
arbitrairement proches de la borne supérieure.
Proposition Soit  une partie non vide de
une partie non vide de 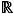 .
.
Si  est majorée, alors
est majorée, alors 
Si  est minorée, alors
est minorée, alors 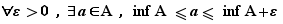
Comme 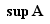 est le plus petit des majorants,
est le plus petit des majorants,  ne peut pas être un majorant. Il existe donc un élément de
ne peut pas être un majorant. Il existe donc un élément de  supérieur à
supérieur à  . Comme
. Comme 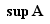 est un majorant, cet élément est inférieur à
est un majorant, cet élément est inférieur à 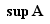 . Le raisonnement pour
. Le raisonnement pour 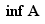 est analogue.
est analogue.
Nous allons souvent rencontrer dans ce cours des réels 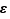 strictement positifs arbitrairement petits. On peut s'en faire une idée concrète en pensant
strictement positifs arbitrairement petits. On peut s'en faire une idée concrète en pensant 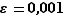 , ou bien
, ou bien 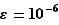 . Prenons comme exemple
. Prenons comme exemple 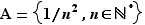 . La borne inférieure est
. La borne inférieure est 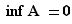 . La proposition permet d'affirmer que pour tout
. La proposition permet d'affirmer que pour tout 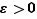 , il existe un élément de l'ensemble inférieur à
, il existe un élément de l'ensemble inférieur à 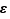 . Et d'ailleurs l'équivalence ci-dessous permet de l'exhiber.
. Et d'ailleurs l'équivalence ci-dessous permet de l'exhiber. 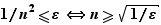
Pour 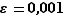 ,
, 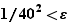 .
.
La proposition admet la réciproque suivante.
Proposition Soit  une partie non vide de
une partie non vide de  .
.
Si  est un majorant de
est un majorant de  tel que
tel que 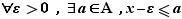 alors
alors 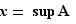 .
.
Si  est un minorant de
est un minorant de  tel que
tel que 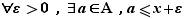 alors
alors 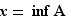 .
.
Si 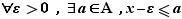 alors pour tout
alors pour tout 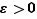 ,
, 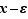 n'est pas un majorant de
n'est pas un majorant de  , donc si
, donc si  est un majorant, c'est bien le plus petit.
est un majorant, c'est bien le plus petit.
Le raisonnement pour 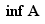 est analogue.
est analogue.
La borne supérieure peut donc être caractérisée de deux manières différentes.

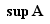 est le plus petit des majorants de
est le plus petit des majorants de 

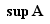 est le seul majorant
est le seul majorant  de
de  tel que pour tout
tel que pour tout 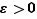 , il existe un élément de
, il existe un élément de  entre
entre 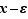 et
et  .
.
De manière analogue,

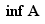 est le plus grand des minorants de
est le plus grand des minorants de 

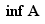 est le seul minorant
est le seul minorant  de
de  tel que pour tout
tel que pour tout 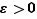 , il existe un élément de
, il existe un élément de  entre
entre  et
et 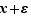 .
.
En liaison avec la proposition précédente, voici pour terminer cette section une application simple des notions de borne supérieure et inférieure, que l'on retrouve dans beaucoup de démonstrations.
Proposition Soient 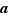 et
et 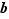 deux réels.
deux réels.
Si pour tout 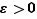 ,
, 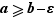 alors
alors 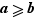 .
.
Si pour tout 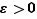 ,
, 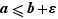 alors
alors  .
.
Considérons la première affirmation. l'ensemble 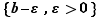 a pour borne supérieure
a pour borne supérieure 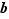 . L'hypothèse affirme que
. L'hypothèse affirme que 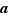 est un majorant de cet ensemble. Il est donc supérieur ou égal à la borne supérieure, par définition de celle-ci. Or d'après la proposition, la borne supérieure de
est un majorant de cet ensemble. Il est donc supérieur ou égal à la borne supérieure, par définition de celle-ci. Or d'après la proposition, la borne supérieure de 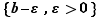 est
est 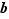 . La seconde affirmation est analogue.
. La seconde affirmation est analogue.
L'ensemble 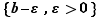 de la démonstration précédente est un intervalle de
de la démonstration précédente est un intervalle de 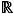 . Nous les décrivons dans la section suivante.
. Nous les décrivons dans la section suivante.
3. Intervalles
Définition Une partie 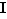 de
de 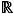 est un intervalle si, dès qu'elle contient deux réels, elle contient tous les réels intermédiaires :
est un intervalle si, dès qu'elle contient deux réels, elle contient tous les réels intermédiaires : 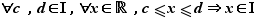
Par exemple, 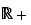 est un intervalle, car tout réel compris entre deux réels positifs est positif. Mais
est un intervalle, car tout réel compris entre deux réels positifs est positif. Mais 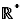 n'en est pas un, car il contient
n'en est pas un, car il contient 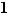 et
et 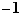 sans contenir
sans contenir 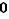 . L'ensemble vide et les singletons sont des cas très particuliers d'intervalles. Nous allons utiliser
. L'ensemble vide et les singletons sont des cas très particuliers d'intervalles. Nous allons utiliser 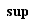 et
et 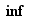 pour caractériser tous les intervalles contenant au moins deux éléments. Ils se répartissent en 9 types, décrits dans le tableau ci-dessous. Dans ce tableau,
pour caractériser tous les intervalles contenant au moins deux éléments. Ils se répartissent en 9 types, décrits dans le tableau ci-dessous. Dans ce tableau, 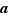 et
et 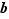 désignent deux réels tels que
désignent deux réels tels que 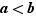 .
.
 |
 |
 |
 |
 |
 |
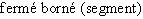 |
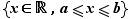 |
![[a,b]](_nb-reels.html/image140.png) |
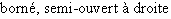 |
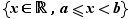 |
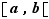 |
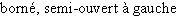 |
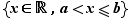 |
![]a,b]](_nb-reels.html/image146.png) |
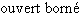 |
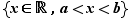 |
![]a,b[](_nb-reels.html/image149.png) |
 |
 |
 |
 |
 |
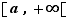 |
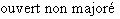 |
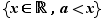 |
![]a,+∞[](_nb-reels.html/image155.png) |
 |
 |
 |
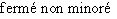 |
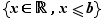 |
![]-∞,b]](_nb-reels.html/image158.png) |
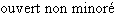 |
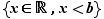 |
![]-∞,b[](_nb-reels.html/image161.png) |
 |
 |
 |
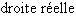 |
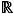 |
![]-∞,+∞[](_nb-reels.html/image163.png) |
Voici la discussion pour les intervalles bornés. Si un intervalle 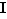 est borné et contient deux éléments, il admet une borne inférieure et une borne supérieure distinctes. Notons
est borné et contient deux éléments, il admet une borne inférieure et une borne supérieure distinctes. Notons  Par définition de
Par définition de 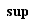 et
et 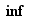 , tout élément
, tout élément  de
de 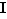 est entre
est entre 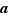 et
et 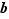 :
: 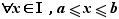 Nous allons montrer que tout réel
Nous allons montrer que tout réel  tel que
tel que 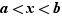 appartient à
appartient à 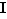 . En effet, si
. En effet, si 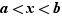 ,
,  n'est ni un majorant, ni un minorant de
n'est ni un majorant, ni un minorant de 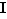 . Il existe donc deux éléments
. Il existe donc deux éléments 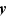 et
et  de
de 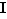 tels que
tels que 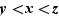 . Par la définition def:intervalle,
. Par la définition def:intervalle,  appartient à
appartient à 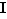 . Selon que
. Selon que 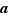 et
et 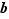 appartiennent ou non à
appartiennent ou non à 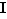 , on obtient les 4 premiers types du tableau.
, on obtient les 4 premiers types du tableau.
Considérons maintenant un intervalle minoré mais non majoré. Soit 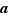 la borne inférieure. Tout élément de
la borne inférieure. Tout élément de 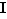 est supérieur ou égal à
est supérieur ou égal à 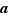 . Montrons que
. Montrons que 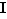 contient tous les réels
contient tous les réels  strictement supérieurs à
strictement supérieurs à 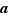 . Comme
. Comme  n'est pas un minorant,
n'est pas un minorant, 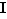 contient un élément
contient un élément  , et comme
, et comme 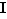 n'est pas majoré, il contient un élément
n'est pas majoré, il contient un élément 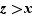 . Donc
. Donc  appartient à
appartient à 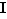 . Selon que
. Selon que 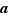 appartient ou non à
appartient ou non à 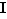 , on obtient
, on obtient 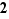 types d'intervalles non majorés. Les deux types d'intervalles non minorés sont analogues.
types d'intervalles non majorés. Les deux types d'intervalles non minorés sont analogues.
Enfin, si un intervalle 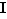 n'est ni majoré, ni minoré, pour tout réel
n'est ni majoré, ni minoré, pour tout réel  , on peut trouver deux réels
, on peut trouver deux réels 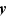 et
et  dans
dans 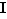 tels que
tels que 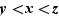 , ce qui entraîne
, ce qui entraîne 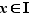 . Donc
. Donc  .
.
4. Rationnels et irrationnels
Un nombre rationnel est le quotient de deux entiers relatifs. La somme de deux rationnels, ainsi que leur produit, sont des rationnels. Muni de l'addition et de la multiplication,  est un corps commutatif totalement ordonné, comme
est un corps commutatif totalement ordonné, comme 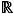 . En revanche,
. En revanche,  ne possède pas la propriété de la borne supérieure. L'ensemble des rationnels dont le carré est inférieur ou égal à
ne possède pas la propriété de la borne supérieure. L'ensemble des rationnels dont le carré est inférieur ou égal à 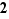 est non vide, majoré, mais il n'a pas de borne supérieure dans
est non vide, majoré, mais il n'a pas de borne supérieure dans  , car
, car 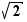 est irrationnel. C'est une application du résultat suivant.
est irrationnel. C'est une application du résultat suivant.
Proposition Soient  et
et 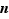 deux entiers strictement positifs. Le nombre
deux entiers strictement positifs. Le nombre  est soit entier, soit irrationnel.
est soit entier, soit irrationnel.
Nous allons démontrer que si  est rationnel, alors il est entier. Soient
est rationnel, alors il est entier. Soient 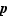 et
et 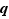 deux entiers premiers entre eux tels que
deux entiers premiers entre eux tels que 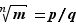 . Alors,
. Alors,  . Mais alors
. Mais alors 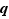 divise
divise 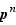 , or
, or 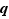 et
et 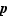 sont premiers entre eux. Ce n'est possible que si
sont premiers entre eux. Ce n'est possible que si 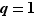 et
et 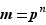 .
.
Observons que la somme d'un rationnel et d'un irrationnel est irrationnelle ; il en est de même pour leur produit. Par contre la somme ou le produit de deux irrationnels peuvent être rationnels (par exemple 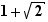 et
et  ).
).
Les rationnels et les irrationnels sont intimement mêlés, comme le montre le théorème suivant.
Théorème Si un intervalle de 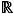 contient au moins deux points distincts, il contient au moins un rationnel et un irrationnel.
contient au moins deux points distincts, il contient au moins un rationnel et un irrationnel.
On traduit cette propriété en disant que  et
et 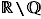 sont denses dans
sont denses dans 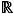 .
.
Soit 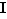 un intervalle contenant deux points
un intervalle contenant deux points 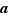 et
et 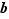 , tels que
, tels que 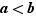 . Soit
. Soit 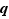 un entier strictement supérieur à
un entier strictement supérieur à 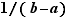 et
et 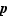 le plus petit entier strictement supérieur à
le plus petit entier strictement supérieur à 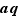 . On a donc :
. On a donc : 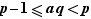 et comme
et comme 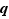 est strictement positif,
est strictement positif, 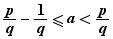 D'où :
D'où : 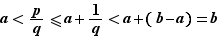 Donc l'intervalle
Donc l'intervalle ![]a,b[](_nb-reels.html/image149.png) , inclus dans
, inclus dans 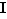 , contient le rationnel
, contient le rationnel 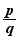 .
.
De même, l'intervalle ![]a/√2,b/√2[](_nb-reels.html/image194.png) contient un rationnel
contient un rationnel  ; donc
; donc ![]a,b[](_nb-reels.html/image149.png) contient
contient 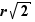 , qui est irrationnel.
, qui est irrationnel.
En fait, tout intervalle contenant au moins deux points contient une infinité de rationnels et une infinité d'irrationnels.
Les rationnels que l'on manipule le plus souvent sont les nombres décimaux, qui sont les multiples entiers de  , où
, où 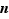 est le nombre de chiffres après la virgule :
est le nombre de chiffres après la virgule : 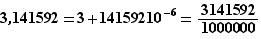 Les nombres décimaux sont le moyen le plus courant d'approcher les réels.
Les nombres décimaux sont le moyen le plus courant d'approcher les réels.
5. Approximation des réels
Nous définissons d'abord les outils de base de l'approximation que sont la valeur absolue, la distance et la partie entière.
La valeur absolue d'un réel  , notée
, notée 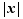 , est
, est 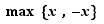 . Elle est égale à
. Elle est égale à  si
si  est positif,
est positif, 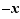 si
si  est négatif.
est négatif.
Si  et
et 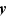 sont deux réels quelconques, la valeur absolue du produit
sont deux réels quelconques, la valeur absolue du produit 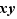 est le produit des valeurs absolues ;
est le produit des valeurs absolues ; 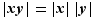 . Par contre, on peut seulement encadrer la valeur absolue de la somme.
. Par contre, on peut seulement encadrer la valeur absolue de la somme.
Proposition Soient  et
et 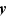 deux réels quelconques. La valeur absolue de leur somme est majorée par la somme des valeurs absolues, et minorée par la différence des valeurs absolues.
deux réels quelconques. La valeur absolue de leur somme est majorée par la somme des valeurs absolues, et minorée par la différence des valeurs absolues. 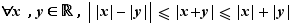 .
.
Quitte à échanger  et
et 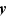 , nous pouvons supposer sans perte de généralité que
, nous pouvons supposer sans perte de généralité que 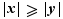 . Si l'un des deux est nul, alors les inégalités sont vérifiées : ce sont des égalités. Sinon, il suffit d'examiner les 4 cas possibles selon le signe de
. Si l'un des deux est nul, alors les inégalités sont vérifiées : ce sont des égalités. Sinon, il suffit d'examiner les 4 cas possibles selon le signe de  et
et 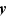 .
.
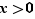 et
et 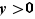 :
: 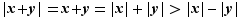
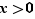 et
et 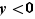 :
: 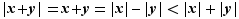
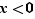 et
et 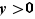 :
: 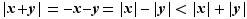
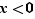 et
et 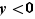 :
: 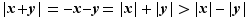
Observez que dans tous les cas, l'une des deux inégalités est une égalité, mais ce n'est pas toujours la même.
En remplaçant 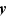 par
par 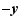 , on obtient le même encadrement pour la valeur absolue d'une différence.
, on obtient le même encadrement pour la valeur absolue d'une différence. 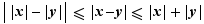 On appelle distance entre deux réels
On appelle distance entre deux réels  et
et 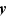 la valeur absolue de leur différence. La proposition appliquée à
la valeur absolue de leur différence. La proposition appliquée à 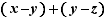 , entraîne :
, entraîne : 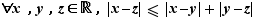 Pour aller d'un point à un autre, on ne peut qu'allonger le parcours si on s'impose de passer par un troisième : c'est l'inégalité triangulaire.
Pour aller d'un point à un autre, on ne peut qu'allonger le parcours si on s'impose de passer par un troisième : c'est l'inégalité triangulaire.
Étant donné un réel  et un réel
et un réel 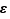 strictement positif, nous dirons que
strictement positif, nous dirons que 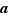 est une approximation (ou une valeur approchée) de
est une approximation (ou une valeur approchée) de  «à
«à 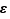 près» si la distance de
près» si la distance de 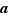 à
à  est inférieure à
est inférieure à 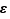 , ce qui équivaut à dire que
, ce qui équivaut à dire que  appartient à l'intervalle
appartient à l'intervalle ![]a-ε,a+ε[](_nb-reels.html/image218.png) .
. ![|x-a|<ε<=>x∈]a-...](_nb-reels.html/image219.png) Les approximations décimales se construisent à l'aide de la partie entière. La partie entière d'un réel
Les approximations décimales se construisent à l'aide de la partie entière. La partie entière d'un réel  est le plus grand entier inférieur ou égal à
est le plus grand entier inférieur ou égal à  . On le note
. On le note 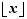 :
: 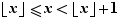 On en déduit :
On en déduit : 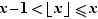 La partie entière de
La partie entière de 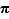 est
est 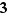 . Attention : la partie entière de
. Attention : la partie entière de 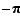 est
est  , et non
, et non  . On appelle partie décimale de
. On appelle partie décimale de  et on note
et on note 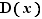 , la différence de
, la différence de  avec sa partie entière.
avec sa partie entière. 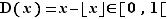
Soit  un réel, et
un réel, et 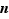 un entier. Considérons la partie entière de
un entier. Considérons la partie entière de 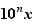 :
:  donc,
donc,  Le nombre décimal
Le nombre décimal 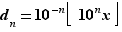 est l'approximation de
est l'approximation de  par défaut à
par défaut à  près. Observez que
près. Observez que 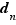 et
et 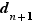 coïncident jusqu'à la dernière décimale de
coïncident jusqu'à la dernière décimale de 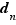 :
: 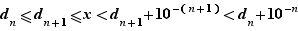
Par exemple, pour 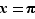 ,
, 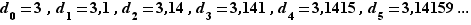
Réciproquement, la donnée d'une suite de décimaux  , telle que
, telle que
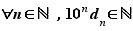
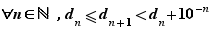
détermine un réel  tel que pour tout
tel que pour tout 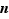
 . La suite
. La suite  est croissante et converge vers
est croissante et converge vers  . Notez
. Notez 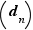 peut déterminer un réel dont elle n'est pas la suite d'approximations décimales, dans le cas où
peut déterminer un réel dont elle n'est pas la suite d'approximations décimales, dans le cas où  est lui même décimal :
est lui même décimal :  En théorie, on peut approcher un réel
En théorie, on peut approcher un réel  par un nombre décimal à n'importe quelle précision. En pratique, la précision habituelle sur des calculs d'ordinateurs est de l'ordre de
par un nombre décimal à n'importe quelle précision. En pratique, la précision habituelle sur des calculs d'ordinateurs est de l'ordre de 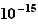 .
.
6. Construction des bornes
Le but de cette section est de démontrer le théorème : toute partie non vide et majorée de 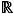 admet une borne supérieure et toute partie non vide et minorée admet une borne inférieure. Soit
admet une borne supérieure et toute partie non vide et minorée admet une borne inférieure. Soit  une partie non vide et majorée de
une partie non vide et majorée de 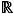 :
:  Si
Si 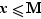 , alors
, alors 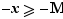 .
.
Si  est non vide et majorée, alors
est non vide et majorée, alors 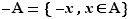 est une partie non vide et minorée. Si la borne supérieure de
est une partie non vide et minorée. Si la borne supérieure de  (plus petit des majorants de
(plus petit des majorants de  ) existe, alors la borne inférieure de
) existe, alors la borne inférieure de 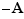 (plus grand des minorants) existe aussi et réciproquement ; de sorte que nous nous dispenserons de démontrer l'existence de la borne inférieure.
(plus grand des minorants) existe aussi et réciproquement ; de sorte que nous nous dispenserons de démontrer l'existence de la borne inférieure.
La démontration va consister à construire explicitement la borne supérieure, en déterminant ses approximations décimales par défaut. Nous vérifierons ensuite que le réel ainsi construit est bien le plus petit des majorants.
Soit  une partie non vide de
une partie non vide de 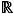 et
et 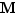 un majorant de
un majorant de  . Pour tout
. Pour tout 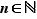 , l'ensemble
, l'ensemble 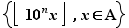 est un ensemble d'entiers, majoré par
est un ensemble d'entiers, majoré par 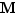 . Il admet donc un plus grand élément. Divisons chacun de ses éléments par
. Il admet donc un plus grand élément. Divisons chacun de ses éléments par  :
: 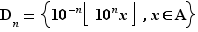 L'ensemble
L'ensemble  est l'ensemble des approximations par défaut à
est l'ensemble des approximations par défaut à  près des éléments de
près des éléments de  . Comme le précédent, il admet un plus grand élément, que nous noterons
. Comme le précédent, il admet un plus grand élément, que nous noterons 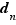 . Par construction, pour tout
. Par construction, pour tout 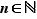 ,
,  . Nous allons démontrer par l'absurde que
. Nous allons démontrer par l'absurde que 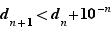 Si ce n'était pas le cas, il existerait
Si ce n'était pas le cas, il existerait  tel que
tel que  Mais alors
Mais alors 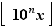 serait supérieur ou égal à
serait supérieur ou égal à 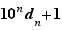 , ce qui contredit la définition de
, ce qui contredit la définition de 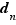 . La suite
. La suite  est donc bien une suite d'approximations décimales et détermine un réel unique que nous notons
est donc bien une suite d'approximations décimales et détermine un réel unique que nous notons 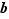 . Nous voulons montrer
. Nous voulons montrer 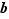 est la borne supérieure de
est la borne supérieure de  . Montrons d'abord que c'est un majorant de
. Montrons d'abord que c'est un majorant de  . Toujours par l'absurde, supposons qu'il existe
. Toujours par l'absurde, supposons qu'il existe  tel que
tel que 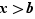 . Fixons
. Fixons 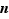 tel que
tel que  . Alors
. Alors 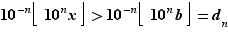 ce qui contredit la définition de
ce qui contredit la définition de 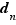 . Il nous reste à montrer que pour tout
. Il nous reste à montrer que pour tout 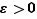 , il existe
, il existe  tel que
tel que 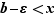 . Fixons
. Fixons 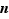 tel que
tel que 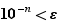 . Par construction, il existe
. Par construction, il existe  tel que
tel que 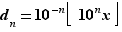 . Donc
. Donc 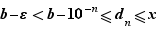
Ne nous leurrons pas : la démonstration qui précède, si elle présente l'avantage de construire explicitement la borne supérieure, n'est pas parfaitement étanche. Vous avez dû admettre qu'une suite d'approximations décimales détermine un réel, ce qui pour être parfaitement intuitif, n'en est pas moins un acte de foi. Pour le justifier, il vous manque une construction axiomatique de l'ensemble des réels, que nous vous raconterons certainement un jour, mais qui pour l'heure dépasse sensiblement le niveau de ce chapitre.