Site http://www.epsilon-publi.net/
- espace http://www.epsilon-publi.net/b/bycart/ de B. Ycart, professeur de mathématique, Université Joseph-Fourier
|
Pour visualiser le document avec epsilonwriter, cliquer ici |
Limites et continuité
Bernard Ycart
Licence CC-BY
Origine : M@ths en ligne - Université Joseph Fourier
Document produit en ouvrant un fichier Tex
Mots-clés: convergence, limite, opération, comparaison, continuité
Sommaire
1. Vocabulaire
Une fonction  de
de  dans
dans  est définie par son graphe : c'est un sous-ensemble
est définie par son graphe : c'est un sous-ensemble 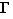 de
de 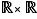 , tel que pour tout
, tel que pour tout  , au plus un réel
, au plus un réel  vérifie
vérifie 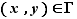 . S'il existe, ce réel
. S'il existe, ce réel  est l'image de
est l'image de  et est noté
et est noté 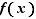 . L'ensemble des
. L'ensemble des  qui ont une image par
qui ont une image par  est le domaine de définition de
est le domaine de définition de  . Nous le noterons
. Nous le noterons 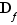 . La notation standard est la suivante :
. La notation standard est la suivante :
 |
 |
|
 |
 |
 |
 |
 |
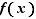 |
Si 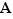 est un sous-ensemble de
est un sous-ensemble de 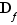 , l'image de
, l'image de 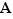 , notée
, notée 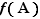 , est l'ensemble des images des éléments de
, est l'ensemble des images des éléments de  .
.
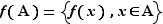
Si 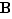 est un sous-ensemble de
est un sous-ensemble de  , l'image réciproque de
, l'image réciproque de 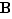 , notée
, notée  , est l'ensemble des antécédents des éléments de
, est l'ensemble des antécédents des éléments de 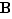 .
.
Attention à la notation 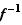 :
:  est défini même si
est défini même si  n'est pas bijective. Par exemple, si
n'est pas bijective. Par exemple, si  est l'application valeur absolue,
est l'application valeur absolue, 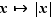 ,
,
![f(]-2,1[)=[0,2[ et f^-1(...](_limites.html/image22.png)
Définition 1 Soit  une fonction, de domaine de définition
une fonction, de domaine de définition 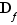 , à valeurs dans
, à valeurs dans  . On dit que
. On dit que  est :
est :
 constante si
constante si 
 croissante si
croissante si 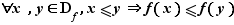
 décroissante si
décroissante si 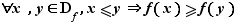
 strictement croissante si
strictement croissante si 
 strictement décroissante si
strictement décroissante si 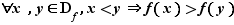
 monotone si elle est croissante ou décroissante
monotone si elle est croissante ou décroissante
 majorée si
majorée si 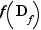 est majoré
est majoré
 minorée si
minorée si 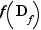 est minoré
est minoré
 bornée si
bornée si 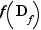 est borné
est borné
Le plus souvent, ces définitions s'appliqueront à des restrictions de  à un intervalle
à un intervalle  inclus dans
inclus dans 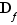 .
.
 |
 |
|
 |
 |
 |
 |
 |
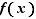 |
Définition 2 Soit  une fonction de
une fonction de  dans
dans  et
et  . Soit
. Soit 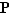 une des propriétés de la définition def:vocabfonction. On dit que
une des propriétés de la définition def:vocabfonction. On dit que  possède la propriété
possède la propriété 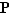
 au voisinage de
au voisinage de  s'il existe un intervalle ouvert
s'il existe un intervalle ouvert 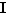 contenant
contenant  , tel que la restriction de
, tel que la restriction de  à
à 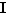 possède la propriété
possède la propriété 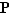 .
.
 au voisinage de
au voisinage de  s'il existe un réel
s'il existe un réel  tel que la restriction de
tel que la restriction de  à
à ![]A,+∞[](_limites.html/image35.png) possède la propriété
possède la propriété 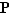 .
.
 au voisinage de
au voisinage de  s'il existe un réel
s'il existe un réel 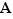 tel que la restriction de
tel que la restriction de  à
à ![]-∞,A[](_limites.html/image37.png) possède la propriété
possède la propriété 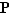 .
.
Par exemple, la fonction valeur absolue 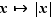 , est :
, est :
 décroissante au voisinage de
décroissante au voisinage de 
 décroissante au voisinage de
décroissante au voisinage de 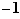
 croissante au voisinage de
croissante au voisinage de 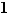
 croissante au voisinage de
croissante au voisinage de 
 bornée au voisinage de
bornée au voisinage de 
Les opérations sur les réels s'étendent aux fonctions de manière naturelle.
 addition :
addition :
 |
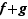 |
|
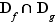 |
 |
 |
 |
 |
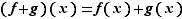 |
 multiplication :
multiplication :
 |
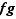 |
|
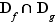 |
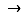 |
 |
 |
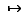 |
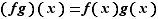 |
 multiplication par un réel :
multiplication par un réel :
 |
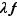 |
|
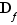 |
 |
 |
 |
 |
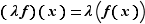 |
 comparaison :
comparaison :
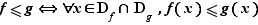
L'addition a les mêmes propriétés que celle des réels : l'ensemble des fonctions de  dans
dans  muni de l'addition est un groupe commutatif. Muni de l'addition et de la multiplication par un réel, c'est un espace vectoriel. Cependant, le produit de deux fonctions peut être nul sans que les deux fonctions le soient.
muni de l'addition est un groupe commutatif. Muni de l'addition et de la multiplication par un réel, c'est un espace vectoriel. Cependant, le produit de deux fonctions peut être nul sans que les deux fonctions le soient.
2. Convergence
Nous commençons par la convergence en un point, vers une limite finie. Afin d'éviter les cas pathologiques, nous supposerons toujours que les fonctions étudiées sont définies au voisinage du point considéré (cf. définition 2).
Définition 3 Soit  un réel et
un réel et  une fonction définie au voisinage de
une fonction définie au voisinage de  , sauf peut-être en
, sauf peut-être en  , et à valeurs dans
, et à valeurs dans  . Soit
. Soit  un réel. On dit que
un réel. On dit que  tend vers
tend vers  quand
quand  tend vers
tend vers  , ou que
, ou que  a pour limite
a pour limite  en
en  si
si
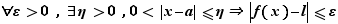
On notera :
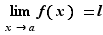 ou bien
ou bien 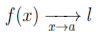
Tout intervalle centré en  contient toutes les valeurs
contient toutes les valeurs 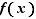 , pour
, pour  suffisamment proche de
suffisamment proche de  . Observez que
. Observez que  peut très bien ne pas être définie en
peut très bien ne pas être définie en  , et admettre quand même une limite en
, et admettre quand même une limite en  . Voici un premier exemple (figure 1).
. Voici un premier exemple (figure 1).
 |
 |
|
 |
 |
 |
 |
 |
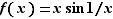 |
Pour tout  ,
, 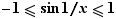 . Donc si
. Donc si 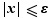 et
et 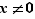 , alors
, alors 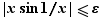 :
:
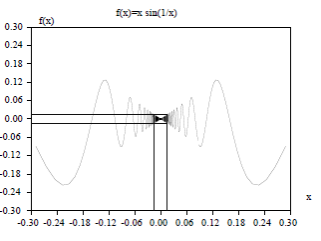
Figure 1 - Graphe de la fonction 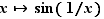
 tend vers
tend vers  quand
quand  tend vers
tend vers  .
.
La convergence peut se caractériser en termes de suites.
Théorème  Soit
Soit  un réel et
un réel et  une fonction définie au voisinage de
une fonction définie au voisinage de  , sauf peut-être en
, sauf peut-être en  , et à valeurs dans
, et à valeurs dans  . Soit
. Soit  un réel. La fonction
un réel. La fonction  tend vers
tend vers  quand
quand  tend vers
tend vers  , si et seulement si, pour toute suite
, si et seulement si, pour toute suite 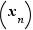 , à valeurs dans
, à valeurs dans  et convergeant vers
et convergeant vers  , la suite
, la suite 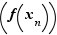 converge vers
converge vers  .
.
Montrons d'abord la condition nécessaire : si  tend vers
tend vers  au sens de la définition 3, alors pour toute suite
au sens de la définition 3, alors pour toute suite 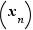 convergeant vers
convergeant vers  , la suite
, la suite 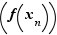 tend vers
tend vers  .
.
Soit 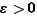 , et
, et  tel que si
tel que si 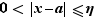 , alors
, alors 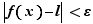 . Soit
. Soit 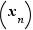 une suite de
une suite de  convergeant vers
convergeant vers  . Il existe
. Il existe 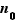 tel que pour tout
tel que pour tout 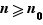 ,
, 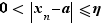 . Mais
. Mais 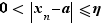 entraîne
entraîne 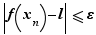 , par hypothèse. Donc la suite
, par hypothèse. Donc la suite 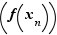 converge vers
converge vers  .
.
Voici maintenant la condition suffisante, dont nous allons démontrer la contraposée : si  ne tend pas vers
ne tend pas vers  , alors il existe une suite
, alors il existe une suite 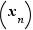 convergeant vers
convergeant vers  telle que la suite
telle que la suite 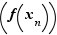 ne tend pas vers
ne tend pas vers  . Ecrivons donc que
. Ecrivons donc que  ne tend pas vers
ne tend pas vers  .
.
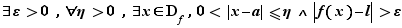
Posons 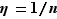 :
:
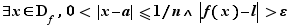
Notons 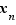 un des réels dont l'existence est affirmée ci-dessus. La suite
un des réels dont l'existence est affirmée ci-dessus. La suite 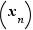 converge vers
converge vers  car
car 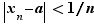 , pourtant la suite
, pourtant la suite 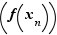 ne tend pas vers
ne tend pas vers  , car
, car 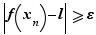 .
.
Voici deux conséquences faciles de la définition.
Proposition 1 Soit  une fonction de
une fonction de  dans
dans  et
et  un réel.
un réel.
Si 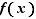 converge quand
converge quand  tend vers
tend vers  , alors la limite est unique.
, alors la limite est unique.
Si 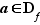 et si
et si  converge vers
converge vers  quand
quand  tend vers
tend vers  , alors
, alors  est bornée au voisinage de
est bornée au voisinage de  .
.
Supposons que  vérifie la définition def:cvfonctionfinie pour deux réels
vérifie la définition def:cvfonctionfinie pour deux réels  et
et  distincts. Posons
distincts. Posons 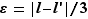 . Alors les intervalles
. Alors les intervalles ![[l-ε,l+ε]](_limites.html/image84.png) et
et ![[l'-ε,l'+ε]](_limites.html/image85.png) sont disjoints. Pour
sont disjoints. Pour  suffisamment proche de
suffisamment proche de  , le réel
, le réel 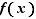 devrait appartenir aux deux intervalles à la fois : c'est impossible.
devrait appartenir aux deux intervalles à la fois : c'est impossible.
Fixons 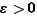 , et
, et  tel que
tel que 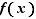 reste dans l'intervalle
reste dans l'intervalle ![]l-ε,l+ε[](_limites.html/image86.png) pour tout
pour tout 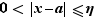 . Alors :
. Alors : ![∀ x∈[a-η,a+η]∩D_f,f(x)≤l...](_limites.html/image87.png) et
et ![∀ x∈[a-η,a+η]∩D_f,f(x)≥l...](_limites.html/image88.png) Donc
Donc  est majorée et minorée au voisinage de
est majorée et minorée au voisinage de  .
.
3. Opérations sur les limites
La notion de limite se combine avec les opérations sur les fonctions comme on l'attend. Nous énoncerons les résultats dans le théorème th:operationslimitesfonctions. Ils peuvent se déduire des résultats analogues sur les suites numériques, via le théorème th:cvepssuite. Nous conseillons au lecteur de le vérifier, puis de comparer cette approche avec les démonstrations directes qui suivent. Elles sont basées sur le lemme suivant.
Lemme 1 Soit  un réel. Soient
un réel. Soient  et
et  deux fonctions de
deux fonctions de  dans
dans  , définies au voisinage de
, définies au voisinage de  , sauf peut-être en
, sauf peut-être en  .
.
Si 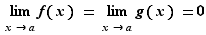 alors
alors 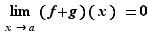
Si  est bornée au voisinage de
est bornée au voisinage de  et
et 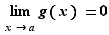 alors
alors 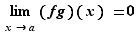
Fixons 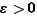 . Soit
. Soit 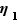 tel que pour
tel que pour 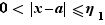 ,
, 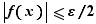 . De même, soit
. De même, soit 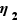 tel que pour
tel que pour  ,
,  . Alors, pour
. Alors, pour 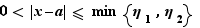 ,
, 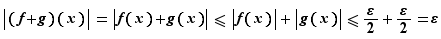 d'où le résultat.
d'où le résultat.
Soit 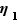 et
et 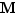 deux réels tels que
deux réels tels que ![∀ x∈[a-η_1,a+η_1],|f(x)|...](_limites.html/image103.png) Fixons
Fixons 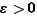 . Soit
. Soit 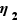 tel que pour
tel que pour  ,
, 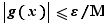 . Alors, pour
. Alors, pour 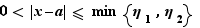 ,
,  d'où le résultat.
d'où le résultat.
Théorème 2 Soit  un réel. Soient
un réel. Soient  et
et  deux fonctions de
deux fonctions de  dans
dans  , définies sur un intervalle ouvert autour de
, définies sur un intervalle ouvert autour de  .
.
Si 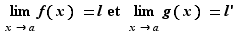 alors
alors 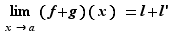
Si 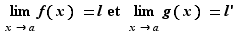 alors
alors 
Pour nous ramener au lemme 1, observons d'abord que 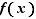 tend vers
tend vers  quand
quand  tend vers
tend vers  , si et seulement si
, si et seulement si 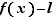 tend vers
tend vers  .
.
Quand  tend vers
tend vers  ,
, 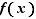 tend vers
tend vers  et
et  tend vers
tend vers 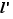 , donc
, donc 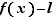 et
et 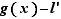 tendent vers
tendent vers  . Donc
. Donc 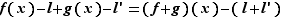 tend vers
tend vers  d'après le point 1. du lemme lem:operationslimitesfonctions. D'où le résultat.
d'après le point 1. du lemme lem:operationslimitesfonctions. D'où le résultat.
Nous voulons montrer que 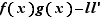 tend vers
tend vers  . Ecrivons :
. Ecrivons : 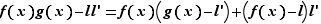 Il suffit de montrer séparément que les deux fonctions
Il suffit de montrer séparément que les deux fonctions 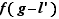 et
et 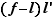 tendent vers
tendent vers  , d'après le premier point du lemme 1. Mais chacune de ces deux fonctions est le produit d'une fonction convergeant vers
, d'après le premier point du lemme 1. Mais chacune de ces deux fonctions est le produit d'une fonction convergeant vers  par une fonction bornée au voisinage de
par une fonction bornée au voisinage de  (
(  est bornée au voisinage de
est bornée au voisinage de  car elle converge). D'où le résultat, par le point 2. du lemme 1.
car elle converge). D'où le résultat, par le point 2. du lemme 1.
Si une application est constante, sa limite en tout point est égale à cette constante. Comme cas particulier du théorème 2, si 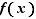 tend vers
tend vers  quand
quand  tend vers
tend vers  , et
, et 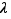 est un réel quelconque, alors la limite en
est un réel quelconque, alors la limite en  de
de 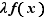 est
est 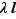 .
.
Le résultat attendu sur la composition des limites se vérifie, à un détail près.
Théorème 3 Soient  et
et  deux réels. Soit
deux réels. Soit  et
et  deux fonctions définies respectivement au voisinage de
deux fonctions définies respectivement au voisinage de  et au voisinage de
et au voisinage de  ,
,  étant définie en
étant définie en  .
.
On suppose : 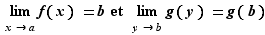 Alors
Alors 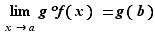
Soit 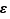 un réel strictement positif. Il existe
un réel strictement positif. Il existe 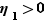 tel que
tel que 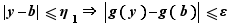
Il existe 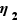 tel que
tel que  Donc :
Donc : 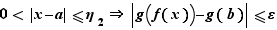
4. Limites unilatérales
Une fonction  peut converger vers une limite finie, comme nous l'avons vu précédemment, ou bien
peut converger vers une limite finie, comme nous l'avons vu précédemment, ou bien  ou
ou  . De plus les valeurs de la variable, qui approchaient
. De plus les valeurs de la variable, qui approchaient  des deux côtés dans les définitions précédentes, peuvent ne l'approcher que d'un seul côté : ce sont les notions de limite à gauche, et de limite à droite. On peut aussi chercher une limite quand
des deux côtés dans les définitions précédentes, peuvent ne l'approcher que d'un seul côté : ce sont les notions de limite à gauche, et de limite à droite. On peut aussi chercher une limite quand  tend vers
tend vers  et
et  . Au total, ce ne sont pas moins de
. Au total, ce ne sont pas moins de 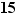 définitions différentes que nous devons donner. Vous reconnaîtrez dans ces définitions un principe général :
définitions différentes que nous devons donner. Vous reconnaîtrez dans ces définitions un principe général : 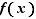 tend vers
tend vers  (fini ou infini) quand
(fini ou infini) quand  tend vers
tend vers  (fini ou infini), si pour tout voisinage
(fini ou infini), si pour tout voisinage 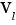 de
de  , il existe un voisinage
, il existe un voisinage  de
de  tel que
tel que 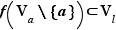 . La définition précise de la notion de voisinage relève de la topologie, et dépasse le cadre de ce cours. Un voisinage de
. La définition précise de la notion de voisinage relève de la topologie, et dépasse le cadre de ce cours. Un voisinage de  sera compris comme un intervalle de la forme
sera compris comme un intervalle de la forme 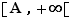 . De même, un voisinage de
. De même, un voisinage de  sera un intervalle de la forme
sera un intervalle de la forme ![]-∞,A]](_limites.html/image133.png) . Un «voisinage à gauche» d'un réel
. Un «voisinage à gauche» d'un réel  sera un intervalle du type
sera un intervalle du type 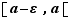 , tandis qu'un «voisinage à droite» sera de la forme
, tandis qu'un «voisinage à droite» sera de la forme ![]a,a+ε]](_limites.html/image135.png) . Nous donnons les différentes définitions sous forme de tableaux. Plutôt que d'apprendre les 5 tableaux par cœur, il est conseillé d'en comprendre le principe pour être capable de retrouver ces définitions en cas de besoin.
. Nous donnons les différentes définitions sous forme de tableaux. Plutôt que d'apprendre les 5 tableaux par cœur, il est conseillé d'en comprendre le principe pour être capable de retrouver ces définitions en cas de besoin.
 |
 |
 |
 |
 |
 |
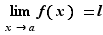 |
 |
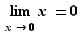 |
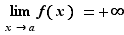 |
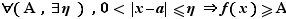 |
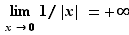 |
 |
||
 |
 |
 |
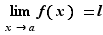 |
 |
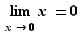 |
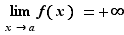 |
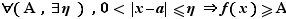 |
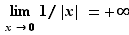 |
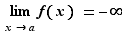 |
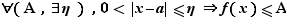 |
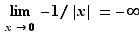 |
 |
||
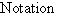 |
 |
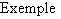 |
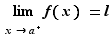 |
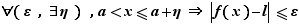 |
 |
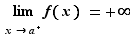 |
 |
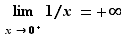 |
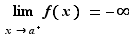 |
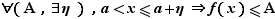 |
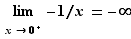 |
La limite bilatérale des sections précédentes peut se caractériser en termes de limites à gauche et à droite.
Proposition 2 Soit  une fonction de
une fonction de  dans
dans  et
et  un réel. La fonction
un réel. La fonction  admet
admet  pour limite en
pour limite en  , si et seulement si elle admet
, si et seulement si elle admet  pour limite à gauche et à droite en
pour limite à gauche et à droite en  .
.
Nous le démontrons pour une limite finie. Ce qui suit est facile à adapter à une limite infinie. La condition nécessaire est évidente au vu des définitions. Pour la condition suffisante, supposons 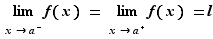
Fixons 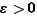 . Il existe
. Il existe 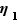 et
et 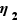 tels que
tels que 
Prenons 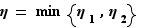 , alors
, alors 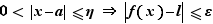
Voici maintenant les définitions des limites en  et
et  .
.
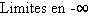 |
 |
|
 |
 |
 |
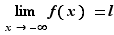 |
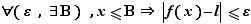 |
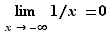 |
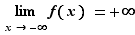 |
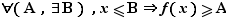 |
 |
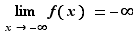 |
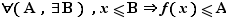 |
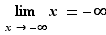 |
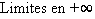 |
||
 |
 |
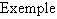 |
 |
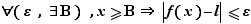 |
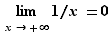 |
 |
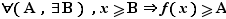 |
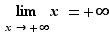 |
 |
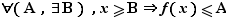 |
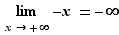 |
Pour chacune de ces définitions, il existe une caractérisation en termes de suites, analogue au théorème 1. Par exemple, la limite à gauche de  en
en  vaut
vaut  si et seulement si pour toute suite
si et seulement si pour toute suite 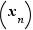 convergeant vers
convergeant vers  et telle que pour tout
et telle que pour tout 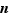 ,
, 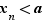 , la suite
, la suite 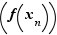 tend vers
tend vers  . Nous laissons au lecteur le soin de démontrer, à titre d'exercice, chacune de ces caractérisations, sur le modèle du théorème 1.
. Nous laissons au lecteur le soin de démontrer, à titre d'exercice, chacune de ces caractérisations, sur le modèle du théorème 1.
En ce qui concerne les opérations, le théorème 2 s'étend aux limites à gauche, à droite, en  et en
et en  , sans aucune difficulté. Les seuls problèmes viennent des limites éventuellement infinies. Dans le cas où les limites de
, sans aucune difficulté. Les seuls problèmes viennent des limites éventuellement infinies. Dans le cas où les limites de  et
et  peuvent être infinies, différentes situations peuvent se produire pour la somme et le produit. Nous les résumons dans les tableaux 1 et 2. Dans ces deux tableaux,
peuvent être infinies, différentes situations peuvent se produire pour la somme et le produit. Nous les résumons dans les tableaux 1 et 2. Dans ces deux tableaux, 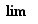 désigne indifféremment une limite bilatérale, à gauche, à droite, en
désigne indifféremment une limite bilatérale, à gauche, à droite, en  ou en
ou en  (du même type pour
(du même type pour  et
et  ). Les points d'interrogations sont des formes indéterminées : tous les cas sont possibles. Par exemple :
). Les points d'interrogations sont des formes indéterminées : tous les cas sont possibles. Par exemple :

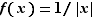 ,
,  :
: 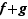 tend vers
tend vers  quand
quand  tend vers
tend vers  .
.

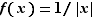 ,
, 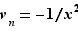 :
: 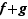 tend vers
tend vers  quand
quand  tend vers
tend vers  .
.

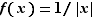 ,
, 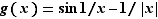 :
: 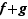 n'a pas de limite en
n'a pas de limite en  .
.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
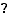 |
 |
Limites possibles de 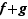 en fonction des limites de
en fonction des limites de  et
et  .
.
 |
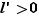 |
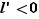 |
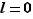 |
 |
 |
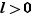 |
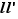 |
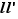 |
 |
 |
 |
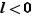 |
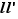 |
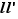 |
 |
 |
 |
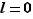 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Limites possibles de 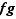 en fonction des limites de
en fonction des limites de  et
et  .
.
Mises à part les formes indéterminées, chacune des cases des tableaux 1 et 2 résume 5 théorèmes : un pour chacun des différents types de limites. Il est conseillé au lecteur de les démontrer, soit directement sur le modèle du théorème 2, soit en utilisant la caractérisation par les suites évoquée plus haut.
5. Convergence des fonctions monotones
Comme pour les suites, «la monotonie entraîne l'existence de limites».
Théorème 4 Soit ![]a,b[](_limites.html/image202.png) un intervalle ouvert, et
un intervalle ouvert, et  une fonction croissante sur
une fonction croissante sur ![]a,b[](_limites.html/image202.png) . Les limites de
. Les limites de  à droite en
à droite en  et à gauche en
et à gauche en  existent et :
existent et :
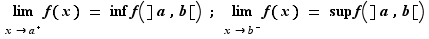
Supposons d'abord que  est minorée :
est minorée : ![f(]a,b[)](_limites.html/image204.png) est une partie minorée de
est une partie minorée de  , elle admet donc une borne inférieure finie, notons-la
, elle admet donc une borne inférieure finie, notons-la  . Soit
. Soit  un réel positif fixé. Par définition de la borne inférieure, il existe
un réel positif fixé. Par définition de la borne inférieure, il existe ![c∈]a,b[](_limites.html/image205.png) tel que
tel que 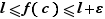 . Mais alors, puisque
. Mais alors, puisque  est croissante,
est croissante,  Donc
Donc  admet
admet  pour limite à droite en
pour limite à droite en  . Si
. Si  n'est pas minorée, pour tout
n'est pas minorée, pour tout  , il existe
, il existe ![c∈]a,b[](_limites.html/image205.png) , tel que
, tel que 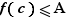 . Puisque
. Puisque  est croissante :
est croissante : 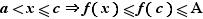 Donc la limite à droite de
Donc la limite à droite de  en
en  est
est  .
.
Pour la limite à gauche en  , on procède de manière analogue, en distinguant le cas où
, on procède de manière analogue, en distinguant le cas où  est majorée, du cas où elle ne l'est pas.
est majorée, du cas où elle ne l'est pas.
L'énoncé du théorème 4, reste vrai si 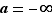 , ou
, ou  . Evidemment, le même résultat vaut pour une fonction décroissante, en inversant le rôle de
. Evidemment, le même résultat vaut pour une fonction décroissante, en inversant le rôle de 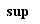 et
et  . On retiendra que
. On retiendra que
toute fonction monotone sur un intervalle admet une limite à gauche et une limite à droite en tout point de cet intervalle.
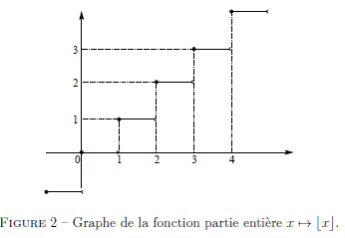
La limite à gauche peut très bien ne pas être égale à la limite à droite. Par exemple, la fonction «partie entière» est croissante sur  , et pour tout
, et pour tout  ,
,
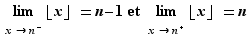
6. Comparaison de fonctions
Dans cette section,  est un réel quelconque, et nous considérons la limite (bilatérale) d'une fonction
est un réel quelconque, et nous considérons la limite (bilatérale) d'une fonction  en
en  , au sens de la définition 3. Toutes les fonctions sont supposées être définies au voisinage de
, au sens de la définition 3. Toutes les fonctions sont supposées être définies au voisinage de  , sauf peut-être en
, sauf peut-être en  .
.
Tous les résultats de la section valent aussi pour des limites à gauche, à droite, en  et en
et en  . L'adaptation des démonstrations aux autres types de limite est un exercice conseillé.
. L'adaptation des démonstrations aux autres types de limite est un exercice conseillé.
Le résultat de base pour comparer deux limites est le suivant.
Théorème 5 Soient  un réel,
un réel,  et
et  deux fonctions définies sur un intervalle ouvert
deux fonctions définies sur un intervalle ouvert 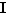 contenant
contenant  . Si pour tout
. Si pour tout  ,
, 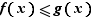 , alors
, alors
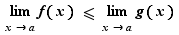
Supposons 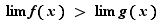 . Alors la limite en
. Alors la limite en  de la fonction
de la fonction 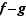 est strictement positive. Notons
est strictement positive. Notons  cette limite. Il existe
cette limite. Il existe  tel que
tel que 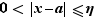 entraîne
entraîne ![f(x)-g(x)∈[l/2,3l/2]](_limites.html/image223.png) , donc
, donc 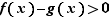 , ce qui contredit l'hypothèse.
, ce qui contredit l'hypothèse.
Le fait de supposer 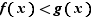 ne renforce pas la conclusion : bien que
ne renforce pas la conclusion : bien que 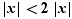 pour tout
pour tout 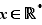 ,
, 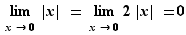
Le théorème 5 ne permet pas de démontrer que l'une des deux fonctions  ou
ou  converge en
converge en  . Pour cela, on utilise souvent le résultat suivant.
. Pour cela, on utilise souvent le résultat suivant.
Théorème 6 Soient  et
et  deux fonctions telles que
deux fonctions telles que  tend vers
tend vers  quand
quand  tend vers
tend vers  . S'il existe un intervalle ouvert
. S'il existe un intervalle ouvert 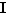 contenant
contenant  tel que pour tout
tel que pour tout  ,
, 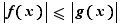 , alors
, alors 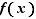 tend vers
tend vers  en
en  .
.
Pour tout 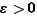 , il existe
, il existe  tel que pour
tel que pour 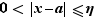 :
:  d'où le résultat.
d'où le résultat.
On en déduit le corollaire suivant.
Corollaire 1 Soient  ,
,  et
et  trois fonctions telles que quand
trois fonctions telles que quand  tend vers
tend vers  ,
, 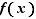 et
et 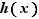 convergent vers la même limite
convergent vers la même limite  . Supposons de plus qu'il existe un intervalle ouvert
. Supposons de plus qu'il existe un intervalle ouvert 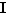 contenant
contenant  , tel que pour tout
, tel que pour tout  ,
, 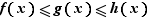 alors
alors  converge vers
converge vers  .
.
Il suffit d'appliquer le théorème th:limite0fonction aux deux fonctions 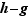 et
et 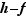 .
.
Soit par exemple
 |
 |
|
 |
 |
 |
 |
 |
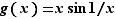 |
Posons 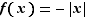 ,
, 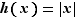 . Les deux fonctions
. Les deux fonctions  et
et  tendent vers
tendent vers  en
en  , et pour tout
, et pour tout 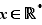 ,
, 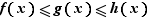 Donc
Donc  tend vers
tend vers  quand
quand  tend vers
tend vers  , comme
, comme  et
et  (cf. figure fig:xsin1).
(cf. figure fig:xsin1).
La comparaison vaut aussi pour les limites infinies.
Théorème 7 Soient  un réel,
un réel,  et
et  deux fonctions définies sur un intervalle ouvert
deux fonctions définies sur un intervalle ouvert 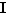 contenant
contenant  . Supposons que, pour tout
. Supposons que, pour tout  ,
, 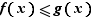 .
.
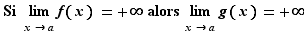
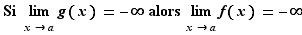
Pour tout  , il existe
, il existe  tel que pour
tel que pour 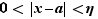 :
: 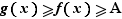 donc
donc  tend vers
tend vers  si
si  tend vers
tend vers  . La démonstration de l'autre affirmation est analogue.
. La démonstration de l'autre affirmation est analogue.
Le vocabulaire de la comparaison des fonctions est analogue à celui des suites, avec la difficulté supplémentaire qu'il faut toujours savoir de quelle limite il s'agit (bilatérale, à gauche, à droite, en  ou en
ou en  ). Nous écrivons la définition ci-dessous pour des limites bilatérales en
). Nous écrivons la définition ci-dessous pour des limites bilatérales en  , elle s'adapte sans problème aux 4 autres types de limites.
, elle s'adapte sans problème aux 4 autres types de limites.
Définition 4 Soient  un réel,
un réel,  et
et  deux fonctions définies sur un intervalle ouvert
deux fonctions définies sur un intervalle ouvert 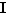 contenant
contenant  .
.
On dit que la fonction  est dominée par la fonction
est dominée par la fonction  au voisinage de
au voisinage de  si :
si : 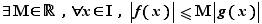 On écrit
On écrit 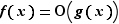 , qui se lit «
, qui se lit « 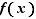 est un grand O de
est un grand O de  » (au voisinage de
» (au voisinage de  ).
).
On dit que la fonction  est négligeable devant la fonction
est négligeable devant la fonction  si :
si : 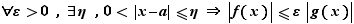 On écrit
On écrit  , qui se lit «
, qui se lit « 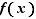 est un petit o de
est un petit o de  » (au voisinage de
» (au voisinage de  ).
).
On dit que la fonction  est équivalente à la fonction
est équivalente à la fonction  si :
si : 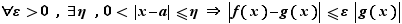 On écrit
On écrit 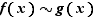 , qui se lit «
, qui se lit « 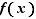 est équivalent à
est équivalent à  » (au voisinage de
» (au voisinage de  ).
).
Très souvent, on appliquera ces définitions pour une fonction  non nulle au voisinage de
non nulle au voisinage de  , sauf peut-être en
, sauf peut-être en  ; dans ce cas, la comparaison se lit sur le rapport
; dans ce cas, la comparaison se lit sur le rapport 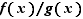 .
.
Proposition 3 Soient  un réel,
un réel,  et
et  deux fonctions définies sur un intervalle ouvert
deux fonctions définies sur un intervalle ouvert  contenant
contenant  . On suppose que la fonction
. On suppose que la fonction  ne s'annule pas sur
ne s'annule pas sur 
 est dominée par
est dominée par  au voisinage de
au voisinage de  si et seulement si le quotient
si et seulement si le quotient  est borné :
est borné :
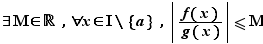
 est négligeable devant
est négligeable devant  si et seulement si le quotient
si et seulement si le quotient  tend vers
tend vers  :
:
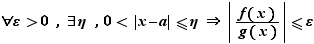
 est équivalente à
est équivalente à  si et seulement si le quotient
si et seulement si le quotient  tend vers
tend vers  :
:
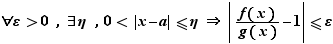
Par exemple, au voisinage de  :
: 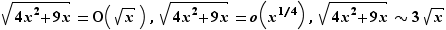
Au voisinage de  :
: 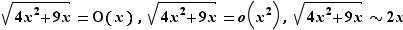
Insistons sur la nécessité de bien préciser le type de limite que l'on considère. Le plus souvent, il s'agira de limites en  ou de limites à droite en
ou de limites à droite en  . On passe des unes aux autres en remplaçant la variable
. On passe des unes aux autres en remplaçant la variable  par
par  . Pour étudier une limite en
. Pour étudier une limite en  , on se ramène à une limite en
, on se ramène à une limite en  en posant
en posant 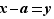 . Le changement de variable
. Le changement de variable 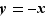 permet de passer des limites à gauche aux limites à droite, des limites en
permet de passer des limites à gauche aux limites à droite, des limites en  aux limites en
aux limites en  .
.
Observons que  entraîne
entraîne 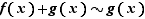 , ce qui est particulièrement utile pour les polynômes. Les équivalents sont souvent utilisés pour le calcul de limites de produits ou de quotients, car si
, ce qui est particulièrement utile pour les polynômes. Les équivalents sont souvent utilisés pour le calcul de limites de produits ou de quotients, car si 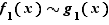 , et
, et 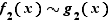 alors
alors 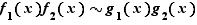 . Par contre il ne faut pas les utiliser pour des sommes. Par exemple, au voisinage de
. Par contre il ne faut pas les utiliser pour des sommes. Par exemple, au voisinage de  :
: 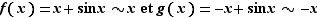 Pourtant,
Pourtant, 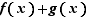 n'est pas équivalent à
n'est pas équivalent à  .
.
Soit  la fonction définie sur
la fonction définie sur ![]0,+∞[](_limites.html/image265.png) par :
par : 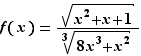
Commençons par les limites à droite en  . Le numérateur tend vers
. Le numérateur tend vers 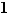 en
en  . Pour le dénominateur
. Pour le dénominateur 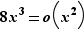 , donc
, donc 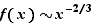 :
: 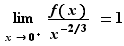
Considérons maintenant les limites en  . Puisque
. Puisque 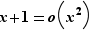 ,
, 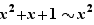 et
et 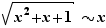 . Pour le dénominateur,
. Pour le dénominateur, 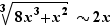 , donc
, donc  tend vers
tend vers  .
. 
Nous admettrons pour l'instant les équivalents suivants au voisinage de  , qui seront justifiés plus loin. Vous devez les connaître par cœur.
, qui seront justifiés plus loin. Vous devez les connaître par cœur.
Théorème 8 Au voisinage de  ,
, 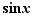 ,
, 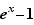 et
et 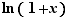 sont équivalents à
sont équivalents à  .
.
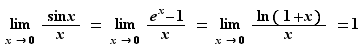
Nous rassemblons dans la section suivante d'autres limites classiques concernant l'exponentielle et le logarithme, qu'il est également bon de connaître.
7. Limites à connaître
Les limites étudiées dans cette section permettent de comparer exponentielles, logarithmes et puissances de  . Vous connaissez certainement déjà le comportement de ces fonctions au voisinage de
. Vous connaissez certainement déjà le comportement de ces fonctions au voisinage de  et de
et de  .
.
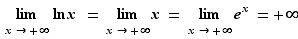
Vous connaissez sans doute aussi le résultat suivant.
Proposition 4 Soit  un réel strictement positif.
un réel strictement positif. 
Posons 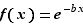 . La fonction
. La fonction  est décroissante, donc elle admet une limite en
est décroissante, donc elle admet une limite en  . Pour identifier cette limite, il suffit de trouver la limite de la suite
. Pour identifier cette limite, il suffit de trouver la limite de la suite 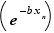 , où
, où 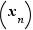 est une suite particulière tendant vers
est une suite particulière tendant vers  . Pour tout
. Pour tout 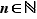 , posons
, posons 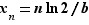 . Comme
. Comme 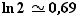 et
et  sont positifs,
sont positifs, 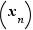 tend vers
tend vers  . On a
. On a 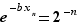 , qui tend vers
, qui tend vers  quand
quand 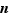 tend vers l'infini.
tend vers l'infini.
Proposition 5 Soient  et
et  deux réels strictement positifs.
deux réels strictement positifs. 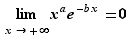
Posons  . L'étude des variations de la fonction
. L'étude des variations de la fonction  sur
sur 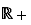 , montre qu'elle est croissante sur
, montre qu'elle est croissante sur ![[0,a/b]](_limites.html/image291.png) , décroissante sur
, décroissante sur 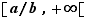 . Comme elle est minorée par
. Comme elle est minorée par  , elle admet une limite en
, elle admet une limite en  . Comme
. Comme 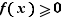 sur
sur ![]0,+∞[](_limites.html/image265.png) , la limite de
, la limite de  en
en  est positive ou nulle. Il nous reste à montrer qu'elle est nulle. Pour cela observons que ce que nous avons dit de
est positive ou nulle. Il nous reste à montrer qu'elle est nulle. Pour cela observons que ce que nous avons dit de  reste vrai si on remplace
reste vrai si on remplace  par
par 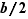 : la fonction qui à
: la fonction qui à  associe
associe 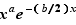 admet un maximum en
admet un maximum en 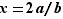 . On a donc :
. On a donc : 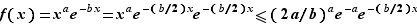 Or
Or 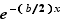 tend vers
tend vers  quand
quand  tend vers
tend vers  (proposition 4). D'où le résultat.
(proposition 4). D'où le résultat.
Ce résultat peut paraître paradoxal : si 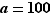 ,
,  croît très vite (
croît très vite ( 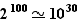 ), et si
), et si 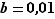 ,
, 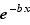 décroît lentement (
décroît lentement ( 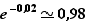 ). Pourtant, c'est l'exponentielle qui finit par l'emporter et la limite en
). Pourtant, c'est l'exponentielle qui finit par l'emporter et la limite en  est nulle.
est nulle.
On retiendra que : l'exponentielle l'emporte sur les puissances de  ,
,
les puissances de  l'emportent sur le logarithme.
l'emportent sur le logarithme.
C'est un moyen mnémotechnique de lever des indéterminations du type 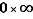 dans les calculs de limite : si l'un des facteurs «l'emporte» sur l'autre, c'est lui qui dicte la limite. Par exemple, dans la proposition proplimab, la limite de
dans les calculs de limite : si l'un des facteurs «l'emporte» sur l'autre, c'est lui qui dicte la limite. Par exemple, dans la proposition proplimab, la limite de 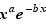 est la même que celle de
est la même que celle de 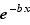 , bien que
, bien que  tende vers
tende vers  . Nous rassemblons dans la proposition ci-après quelques exemples de limites du même type que celle de la proposition proplimab. Toutes s'en déduisent par des changements de variables : c'est un exercice facile que nous vous conseillons.
. Nous rassemblons dans la proposition ci-après quelques exemples de limites du même type que celle de la proposition proplimab. Toutes s'en déduisent par des changements de variables : c'est un exercice facile que nous vous conseillons.
Proposition 6 Soient  et
et  deux réels strictement positifs.
deux réels strictement positifs.
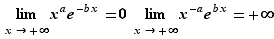
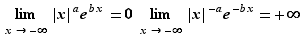
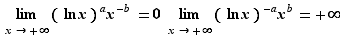
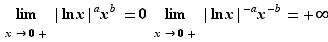
8. Continuité en un point
Une fonction  est continue en
est continue en  quand elle admet
quand elle admet 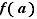 comme limite en
comme limite en  .
.
Définition 5 Soit  un réel et
un réel et  une fonction définie au voisinage de
une fonction définie au voisinage de  . On dit que
. On dit que  est :
est :
continue en  si
si 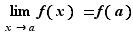 soit :
soit : 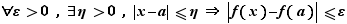
continue à gauche en  si
si 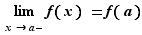 soit :
soit : 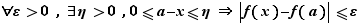
continue à droite en  si
si 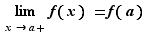 soit :
soit : 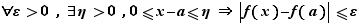
Par exemple la fonction partie entière 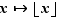 est continue en
est continue en  si
si  n'est pas un entier. Elle est continue à droite (mais pas à gauche) en
n'est pas un entier. Elle est continue à droite (mais pas à gauche) en  si
si  est entier : voir figure 2.
est entier : voir figure 2.
On déduit du théorème th:cvepssuite une caractérisation de la continuité en termes de suites.
Théorème 9 La fonction  est continue en
est continue en  , si et seulement si pour toute suite de réels
, si et seulement si pour toute suite de réels 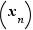 telle que
telle que 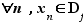 et convergeant vers
et convergeant vers  , la suite
, la suite 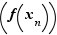 converge vers
converge vers 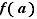 .
.
Observons que si une fonction est continue en un point, elle est nécessairement définie en ce point. Nous avons vu qu'une fonction  pouvait admettre une limite en
pouvait admettre une limite en  , sans être définie en
, sans être définie en  . Si c'est le cas, on appelle prolongement par continuité de
. Si c'est le cas, on appelle prolongement par continuité de  en
en  , la fonction
, la fonction  , définie sur
, définie sur 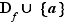 , et telle que
, et telle que
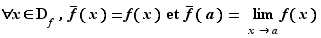
Par exemple,
 |
 |
|
 |
 |
 |
 |
 |
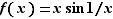 |
Cette fonction peut être prolongée par continuité en  :
:
 |
 |
|
 |
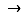 |
 |
 |
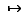 |
 |
 |
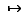 |
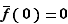 |
Des théorèmes 2 et 3, on déduit que la somme, le produit, la composée de deux fonctions continues sont continues.
Théorème 10 Soient  et
et  deux fonctions. Soit
deux fonctions. Soit  un réel.
un réel.
Si  et
et  sont continues en
sont continues en  , alors
, alors 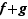 et
et 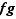 sont continues en
sont continues en  .
.
Si  est continue en
est continue en  et
et  est continue en
est continue en 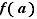 , alors
, alors 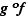 est continue en
est continue en  .
.
Ce théorème permet de démontrer la continuité de toutes les fonctions que vous aurez à examiner, à condition d'admettre la continuité des «briques de base» que sont les fonctions usuelles.
Toutes les fonctions usuelles sont continues en tout point où elles sont définies Ceci concerne les fonctions puissances, exponentielle, logarithme, sinus, cosinus, mais exclut bien sûr la partie entière et la partie décimale.
À titre d'exemple, nous allons le démontrer pour la fonction 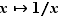 .
.
Proposition 7 La fonction  qui à
qui à  associe
associe  est continue en tout point de
est continue en tout point de 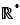 .
.
Soit  un réel non nul. Soit
un réel non nul. Soit 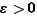 . Notons
. Notons  Si
Si  , alors
, alors  . Donc :
. Donc : 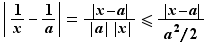 Donc,
Donc,  entraîne
entraîne 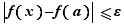 .
.
Les fonctions constantes, ainsi que la fonction identité 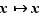 sont évidemment continues en tout point de
sont évidemment continues en tout point de  . Du théorème 10, on déduit qu'il en est de même pour les fonctions polynômes. En utilisant la proposition 7, on obtient que toute fraction rationnelle (quotient de deux fonctions polynômes) est continue en tout point où son dénominateur ne s'annule pas.
. Du théorème 10, on déduit qu'il en est de même pour les fonctions polynômes. En utilisant la proposition 7, on obtient que toute fraction rationnelle (quotient de deux fonctions polynômes) est continue en tout point où son dénominateur ne s'annule pas.
9. Continuité sur un intervalle
Définition 6 Soit  une fonction définie sur un intervalle
une fonction définie sur un intervalle  ouvert non vide de
ouvert non vide de  . On dit que
. On dit que  est continue sur
est continue sur  si
si  est continue en tout point de
est continue en tout point de 
Cette définition comporte une petite ambiguïté pour les intervalles qui ne sont pas ouverts. Nous conviendrons qu'une fonction continue sur ![[a,b]](_limites.html/image335.png) est continue en tout point de
est continue en tout point de ![]a,b[](_limites.html/image202.png) et que de plus, elle est continue à droite en
et que de plus, elle est continue à droite en  et à gauche en
et à gauche en  .
.
Le résultat important de cette section est le théorème des valeurs intermédiaires.
Théorème 11 Soit  un intervalle de
un intervalle de  et
et  une fonction continue sur
une fonction continue sur  . Soit
. Soit 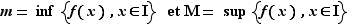
Si 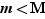 , alors, pour tout réel
, alors, pour tout réel  tel que
tel que 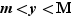 , il existe
, il existe 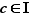 tel que
tel que  .
.
La figure 3 illustre le théorème des valeurs intermédiaires. Le résultat est tout à fait intuitif : si une fonction continue prend deux valeurs distinctes sur un intervalle, elle prend nécessairement toutes les valeurs entre ces deux-là : le graphe d'une fonction continue n'a pas de saut vertical.

Par définition de la borne inférieure, et de la borne supérieure, il existe 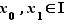 tels que
tels que 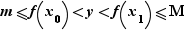 Quitte à remplacer
Quitte à remplacer  par
par 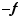 , nous pouvons supposer sans perte de généralité que
, nous pouvons supposer sans perte de généralité que 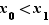 . Soit
. Soit 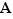 l'ensemble des
l'ensemble des ![x∈[x_0,x_1]](_limites.html/image346.png) tels que
tels que 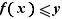 . L'ensemble
. L'ensemble 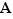 est non vide (il contient
est non vide (il contient 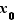 ), et majoré par
), et majoré par 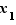 . Donc il admet une borne supérieure finie. Soit
. Donc il admet une borne supérieure finie. Soit 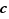 cette borne supérieure.
cette borne supérieure. ![c= sup {x∈[x_0,x_1],f(x)...](_limites.html/image351.png) Nous allons démontrer que
Nous allons démontrer que  , en utilisant la continuité de
, en utilisant la continuité de  . Soit
. Soit 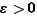 . Puisque
. Puisque  est continue en
est continue en 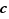 , il existe
, il existe  tel que
tel que 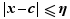 implique
implique  . Or par définition de la borne supérieure, il existe
. Or par définition de la borne supérieure, il existe 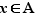 tel que
tel que 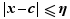 . Fixons un tel
. Fixons un tel  . Puisque
. Puisque  et
et 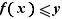 , alors nécessairement
, alors nécessairement 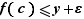 .
.
Par définition de la borne supérieure, 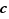 est le plus petit des majorants de
est le plus petit des majorants de  . Fixons maintenant
. Fixons maintenant  tel que
tel que 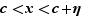 . Alors
. Alors 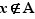 , donc
, donc 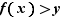 , et
, et  . On en déduit que
. On en déduit que 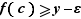 .
.
Nous avons donc démontré que pour tout 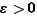 ,
, 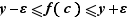 ce qui entraîne
ce qui entraîne  .
.
Les deux résultats suivants sont des formulations équivalentes du théorème des valeurs intermédiaires.
Corollaire 2
 Si une fonction continue sur un intervalle prend des valeurs positives et des valeurs négatives, alors elle s'annule sur cet intervalle.
Si une fonction continue sur un intervalle prend des valeurs positives et des valeurs négatives, alors elle s'annule sur cet intervalle.
 L'image par une application continue d'un intervalle est un intervalle.
L'image par une application continue d'un intervalle est un intervalle.
Il est naturel de se demander si l'image par une application continue d'un intervalle est un intervalle du même type (infini, ouvert...). Le seul résultat général concerne les intervalles fermés bornés.
Théorème 12 Soient 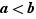 deux réels et
deux réels et  une fonction continue sur
une fonction continue sur ![[a,b]](_limites.html/image335.png) . Soit
. Soit
![m= inf {f(x),x∈[a,b]} et...](_limites.html/image362.png)
Alors 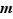 et
et 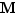 sont finies et il existe
sont finies et il existe ![x_1,x_2∈[a,b]](_limites.html/image364.png) , tels que
, tels que  et
et 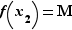 :
:
![f([a,b])=[m,M]](_limites.html/image367.png)
elle utilise le théorème de Bolzano-Weierstrass, qui affirme que de toute suite 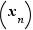 , à valeurs dans l'intervalle
, à valeurs dans l'intervalle ![[a,b]](_limites.html/image335.png) , on peut extraire une sous-suite convergente. Nous traitons la borne supérieure
, on peut extraire une sous-suite convergente. Nous traitons la borne supérieure 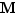 , la démonstration est analogue pour
, la démonstration est analogue pour 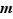 . Supposons
. Supposons 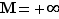 . Pour tout
. Pour tout 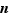 , il existe
, il existe ![x_n∈[a,b]](_limites.html/image369.png) tel que
tel que 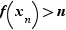 . Donc la suite
. Donc la suite 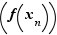 tend vers
tend vers  . De la suite
. De la suite 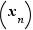 , on peut extraire une sous-suite convergente. Soit
, on peut extraire une sous-suite convergente. Soit 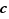 la limite de cette sous-suite. Par la continuité de
la limite de cette sous-suite. Par la continuité de  , les images des termes de la sous-suite convergent vers
, les images des termes de la sous-suite convergent vers  , ce qui contredit le fait que
, ce qui contredit le fait que 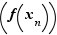 tend vers
tend vers  . Donc
. Donc 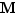 est finie.
est finie.
Puisque la borne supérieure est finie, pour tout 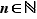 , il existe
, il existe ![x_n∈[a,b]](_limites.html/image369.png) tel que
tel que 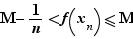 Donc la suite
Donc la suite 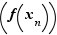 converge vers
converge vers 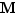 . De la suite
. De la suite 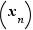 , on peut extraire une sous-suite, convergeant vers
, on peut extraire une sous-suite, convergeant vers ![c∈[a,b]](_limites.html/image373.png) . En utilisant à nouveau la continuité, on en déduit que
. En utilisant à nouveau la continuité, on en déduit que  .
.
En général les bornes 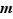 et
et 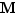 sont différentes des valeurs de
sont différentes des valeurs de  en
en  et
et  . Le cas des fonctions monotones est particulier. Vous avez sans doute déjà rencontré le résultat qui suit sous le nom de théorème de la bijection.
. Le cas des fonctions monotones est particulier. Vous avez sans doute déjà rencontré le résultat qui suit sous le nom de théorème de la bijection.
Théorème 13 Soit  une fonction continue, strictement monotone sur un intervalle
une fonction continue, strictement monotone sur un intervalle 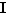 .
.
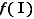 est un intervalle, dont les bornes sont les limites de
est un intervalle, dont les bornes sont les limites de  aux bornes de
aux bornes de 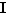
 est une bijection de
est une bijection de 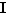 vers
vers 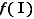
la bijection réciproque 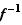 est continue sur
est continue sur 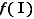 et strictement monotone, de même sens que
et strictement monotone, de même sens que  .
.
Quitte à remplacer  par
par 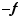 , nous pouvons supposer sans perte de généralité que
, nous pouvons supposer sans perte de généralité que  est strictement croissante. Ceci entraîne que
est strictement croissante. Ceci entraîne que  est injective. Supposons que
est injective. Supposons que 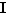 soit l'intervalle ouvert
soit l'intervalle ouvert ![]a,b[](_limites.html/image202.png) ,
,  et
et  étant éventuellement infinis. La démonstration s'adapte sans problème au cas où l'intervalle est fermé d'un côté ou des deux.
étant éventuellement infinis. La démonstration s'adapte sans problème au cas où l'intervalle est fermé d'un côté ou des deux.
Observons que pour tout ![x_0∈]a,b[](_limites.html/image376.png)
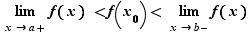 Posons
Posons 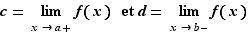 Soit
Soit ![y∈]c,d[](_limites.html/image379.png) . D'après le théorème des valeurs intermédiaires, il existe
. D'après le théorème des valeurs intermédiaires, il existe ![x∈]a,b[](_limites.html/image380.png) tel que
tel que 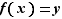 . Donc
. Donc ![f(]a,b[)=]c,d[](_limites.html/image382.png) , et comme
, et comme  est injective, c'est une bijection de
est injective, c'est une bijection de ![]a,b[](_limites.html/image202.png) vers
vers ![]c,d[](_limites.html/image383.png) . Pour tout
. Pour tout ![x_1,x_2∈]a,b[](_limites.html/image384.png) ,
, 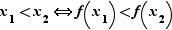 Donc la bijection réciproque
Donc la bijection réciproque 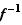 est elle-aussi strictement croissante. Il reste à démontrer qu'elle est continue. Soit
est elle-aussi strictement croissante. Il reste à démontrer qu'elle est continue. Soit ![y_0∈]c,d[](_limites.html/image386.png) et
et  . Soit
. Soit 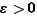 tel que
tel que 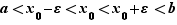 Posons
Posons 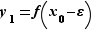 et
et  . Alors
. Alors 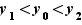 . Soit
. Soit 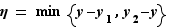 . Pour tout
. Pour tout  tel que
tel que 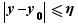 , on a
, on a 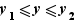 , donc
, donc 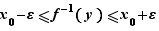 . D'où le résultat.
. D'où le résultat.
Si  est bijective, à tout couple
est bijective, à tout couple  du graphe de
du graphe de  , correspond le couple
, correspond le couple 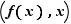 du graphe de
du graphe de 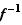 : les deux graphes se déduisent l'un de l'autre par la transformation
: les deux graphes se déduisent l'un de l'autre par la transformation 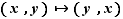 , qui est la symétrie par rapport à la première bissectrice (figure 4).
, qui est la symétrie par rapport à la première bissectrice (figure 4).
